?tzrzf

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 3/22/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-009DF030-771D-46F4-B9F6-01CBC0746003

View Details

?tzrzf

Reduces the upper trapezoidal matrix A to upper triangular form.

Syntax

lapack_int LAPACKE_stzrzf (int matrix_layout, lapack_int m, lapack_int n, float* a, lapack_int lda, float* tau);

lapack_int LAPACKE_dtzrzf (int matrix_layout, lapack_int m, lapack_int n, double* a, lapack_int lda, double* tau);

lapack_int LAPACKE_ctzrzf (int matrix_layout, lapack_int m, lapack_int n, lapack_complex_float* a, lapack_int lda, lapack_complex_float* tau);

lapack_int LAPACKE_ztzrzf (int matrix_layout, lapack_int m, lapack_int n, lapack_complex_double* a, lapack_int lda, lapack_complex_double* tau);

Include Files

mkl.h

Description

The routine reduces the m-by-n (m≤n) real/complex upper trapezoidal matrix A to upper triangular form by means of orthogonal/unitary transformations. The upper trapezoidal matrix A = [A1 A2] = [A_{1:m, 1:m}, A_{1:m, m+1:n}] is factored as

A = [R0]*Z,

where Z is an n-by-n orthogonal/unitary matrix, R is an m-by-m upper triangular matrix, and 0 is the m-by-(n-m) zero matrix.

The ?tzrzf routine replaces the deprecated ?tzrqf routine.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

m

The number of rows in the matrix A (m≥ 0).

n

The number of columns in A (n≥m).

a

Array a is of size max(1, lda*n) for column major layout and max(1, lda*m) for row major layout.

The leading m-by-n upper trapezoidal part of the array a contains the matrix A to be factorized.

lda

The leading dimension of a; at least max(1, m)for column major layout and max(1, n) for row major layout.

Output Parameters

a

Overwritten on exit by the factorization data as follows:

the leading m-by-m upper triangular part of a contains the upper triangular matrix R, and elements m +1 to n of the first m rows of a, with the array tau, represent the orthogonal matrix Z as a product of m elementary reflectors.

tau

Array, size at least max (1, m). Contains scalar factors of the elementary reflectors for the matrix Z.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Application Notes

The factorization is obtained by Householder's method. The k-th transformation matrix, Z(k), which is used to introduce zeros into the (m - k + 1)-th row of A, is given in the form

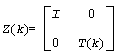
where for real flavors

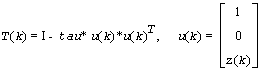
and for complex flavors

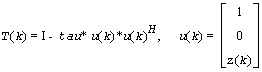
tau is a scalar and z(k) is an l-element vector. tau and z(k) are chosen to annihilate the elements of the k-th row of A2.

The scalar tau is returned in the k-th element of tau and the vector u(k) in the k-th row of A, such that the elements of z(k) are stored in the last m - n elements of the k-th row of array a.

The elements of R are returned in the upper triangular part of A.

The matrix Z is given by

Z = Z(1)*Z(2)*...*Z(m).

Related routines include:

ormrz: to apply matrix Q (for real matrices)
unmrz: to apply matrix Q (for complex matrices).

Parent topic: Orthogonal Factorizations: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?tzrzf

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes