?trsen

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 3/22/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-78D7846A-6330-4301-92C9-DB9D38BF7F28

View Details

?trsen

Reorders the Schur factorization of a matrix and (optionally) computes the reciprocal condition numbers for the selected cluster of eigenvalues and respective invariant subspace.

Syntax

lapack_int LAPACKE_strsen( int matrix_layout, char job, char compq, const lapack_logical* select, lapack_int n, float* t, lapack_int ldt, float* q, lapack_int ldq, float* wr, float* wi, lapack_int* m, float* s, float* sep );

lapack_int LAPACKE_dtrsen( int matrix_layout, char job, char compq, const lapack_logical* select, lapack_int n, double* t, lapack_int ldt, double* q, lapack_int ldq, double* wr, double* wi, lapack_int* m, double* s, double* sep );

lapack_int LAPACKE_ctrsen( int matrix_layout, char job, char compq, const lapack_logical* select, lapack_int n, lapack_complex_float* t, lapack_int ldt, lapack_complex_float* q, lapack_int ldq, lapack_complex_float* w, lapack_int* m, float* s, float* sep );

lapack_int LAPACKE_ztrsen( int matrix_layout, char job, char compq, const lapack_logical* select, lapack_int n, lapack_complex_double* t, lapack_int ldt, lapack_complex_double* q, lapack_int ldq, lapack_complex_double* w, lapack_int* m, double* s, double* sep );

Include Files

mkl.h

Description

The routine reorders the Schur factorization of a general matrix A = Q*T*Q^T (for real flavors) or A = Q*T*Q^H (for complex flavors) so that a selected cluster of eigenvalues appears in the leading diagonal elements (or, for real flavors, diagonal blocks) of the Schur form. The reordered Schur form R is computed by a unitary (orthogonal) similarity transformation: R = Z^H*T*Z. Optionally the updated matrix P of Schur vectors is computed as P = Q*Z, giving A = P*R*P^H.

Let

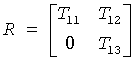
where the selected eigenvalues are precisely the eigenvalues of the leading m-by-m submatrix T₁₁. Let P be correspondingly partitioned as (Q₁Q₂) where Q₁ consists of the first m columns of Q. Then A*Q₁ = Q₁*T₁₁, and so the m columns of Q₁ form an orthonormal basis for the invariant subspace corresponding to the selected cluster of eigenvalues.

Optionally the routine also computes estimates of the reciprocal condition numbers of the average of the cluster of eigenvalues and of the invariant subspace.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

job

Must be 'N' or 'E' or 'V' or 'B'.

If job = 'N', then no condition numbers are required.

If job = 'E', then only the condition number for the cluster of eigenvalues is computed.

If job = 'V', then only the condition number for the invariant subspace is computed.

If job = 'B', then condition numbers for both the cluster and the invariant subspace are computed.

compq

Must be 'V' or 'N'.

If compq = 'V', then Q of the Schur vectors is updated.

If compq = 'N', then no Schur vectors are updated.

select

Array, size at least max (1, n).

Specifies the eigenvalues in the selected cluster. To select an eigenvalue λ_j, select[j] must be 1

For real flavors: to select a complex conjugate pair of eigenvalues λ_j and λ_j+1 (corresponding 2 by 2 diagonal block), select[j - 1] and/or select[j] must be 1; the complex conjugate λ_jand λ_{j + 1} must be either both included in the cluster or both excluded.

n

The order of the matrix T (n≥ 0).

t, q

Arrays:

t (size max(1, ldt*n)) Theupper quasi-triangular n-by-n matrix T, in Schur canonical form.

q (size max(1, ldq*n))

If compq = 'V', then q must contain the matrix Q of Schur vectors.

If compq = 'N', then q is not referenced.

ldt

The leading dimension of t; at least max(1, n).

ldq

The leading dimension of q;

If compq = 'N', then ldq≥ 1.

If compq = 'V', then ldq≥ max(1, n).

Output Parameters

t

Overwritten by the reordered matrix R in Schur canonical form with the selected eigenvalues in the leading diagonal blocks.

q

If compq = 'V', q contains the updated matrix of Schur vectors; the first m columns of the Q form an orthogonal basis for the specified invariant subspace.

w

Array, size at least max(1, n). The recorded eigenvalues of R. The eigenvalues are stored in the same order as on the diagonal of R.

wr, wi

Arrays, size at least max(1, n). Contain the real and imaginary parts, respectively, of the reordered eigenvalues of R. The eigenvalues are stored in the same order as on the diagonal of R. Note that if a complex eigenvalue is sufficiently ill-conditioned, then its value may differ significantly from its value before reordering.

m

For complex flavors: the dimension of the specified invariant subspaces, which is the same as the number of selected eigenvalues (see select).

For real flavors: the dimension of the specified invariant subspace. The value of m is obtained by counting 1 for each selected real eigenvalue and 2 for each selected complex conjugate pair of eigenvalues (see select).

Constraint: 0 ≤m≤n.

s

If job = 'E' or 'B', s is a lower bound on the reciprocal condition number of the average of the selected cluster of eigenvalues.

If m = 0 or n, then s = 1.

For real flavors: if info = 1, then s is set to zero.s is not referenced if job = 'N' or 'V'.

sep

If job = 'V' or 'B', sep is the estimated reciprocal condition number of the specified invariant subspace.

If m = 0 or n, then sep = |T|.

For real flavors: if info = 1, then sep is set to zero.

sep is not referenced if job = 'N' or 'E'.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = 1, the reordering of T failed because some eigenvalues are too close to separate (the problem is very ill-conditioned); T may have been partially reordered, and wr and wi contain the eigenvalues in the same order as in T; s and sep (if requested) are set to zero.

Application Notes

The computed matrix R is exactly similar to a matrix T+E, where ||E||₂ = O(ε)*||T||₂, and ε is the machine precision. The computed s cannot underestimate the true reciprocal condition number by more than a factor of (min(m, n-m))_1/2; sep may differ from the true value by (m*n-m²)_1/2. The angle between the computed invariant subspace and the true subspace is O(ε)*||A||₂/sep. Note that if a 2-by-2 diagonal block is involved in the re-ordering, its off-diagonal elements are in general changed; the diagonal elements and the eigenvalues of the block are unchanged unless the block is sufficiently ill-conditioned, in which case they may be noticeably altered. It is possible for a 2-by-2 block to break into two 1-by-1 blocks, that is, for a pair of complex eigenvalues to become purely real.

Parent topic: Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?trsen

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes