mkl_?getrfnpi

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 3/22/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-70978EF9-49CB-4475-9CDE-DEFB1B9DF910

View Details

mkl_?getrfnpi

Performs LU factorization (complete or incomplete) of a general matrix without pivoting.

Syntax

lapack_int LAPACKE_mkl_sgetrfnpi (int matrix_layout, lapack_int m, lapack_int n, lapack_int nfact, float* a, lapack_int lda);

lapack_int LAPACKE_mkl_dgetrfnpi (int matrix_layout, lapack_int m, lapack_int n, lapack_int nfact, double* a, lapack_int lda);

lapack_int LAPACKE_mkl_cgetrfnpi (int matrix_layout, lapack_int m, lapack_int n, lapack_int nfact, lapack_complex_float* a, lapack_int lda);

lapack_int LAPACKE_mkl_zgetrfnpi (int matrix_layout, lapack_int m, lapack_int n, lapack_int nfact, lapack_complex_double* a, lapack_int lda);

Include Files

mkl.h

Description

The routine computes the LU factorization of a general m-by-n matrix A without using pivoting. It supports incomplete factorization. The factorization has the form:

A = L*U,

where L is lower triangular with unit diagonal elements (lower trapezoidal if m > n) and U is upper triangular (upper trapezoidal if m < n).

Incomplete factorization has the form:

where L is lower trapezoidal with unit diagonal elements, U is upper trapezoidal, and is the unfactored part of matrix A. See the application notes section for further details.

NOTE:

Use ?getrf if it is possible that the matrix is not diagonal dominant.

Input Parameters

A <datatype> placeholder, if present, is used for the C interface data types in the C interface section above. See C Interface Conventions for the C interface principal conventions and type definitions.

matrix_layout: Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).
m: The number of rows in matrix A; m≥ 0.
n: The number of columns in matrix A; n≥ 0.
nfact: The number of rows and columns to factor; 0 ≤nfact≤ min(m, n). Note that if nfact < min(m, n), incomplete factorization is performed.
a: Array of size at least lda*n for column major layout and at least lda*m for row major layout. Contains the matrix A.
lda: The leading dimension of array a. lda≥ max(1, m) for column major layout and lda≥ max(1, n) for row major layout.

Output Parameters

a

Overwritten by L and U. The unit diagonal elements of L are not stored.

When incomplete factorization is specified by setting nfact < min(m, n), a also contains the unfactored submatrix 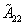. See the application notes section for further details.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = i, u_ii is 0. The requested factorization has been completed, but U is exactly singular. Division by 0 will occur if factorization is completed and factor U is used for solving a system of linear equations.

Application Notes

The computed L and U are the exact factors of a perturbed matrix A + E, with

|E| ≤ c(min(m, n))ε |L||U|

where c(n) is a modest linear function of n, and ε is the machine precision.

The approximate number of floating-point operations for real flavors is

(2/3)`n`³	If `m = n` = nfact
(1/3)`n`²(3`m`-`n`)	If `m>n = nfact`
(1/3)`m`²(3`n`-`m`)	If `m = nfact<n`
(2/3)`n`³ - (`n`-`nfact`)³	If `m = n,nfact< min(m, n)`
(1/3)(`n`²(3`m`-`n`) - (`n`-nfact)²(3`m` - 2nfact - `n`))	If `m>n > nfact`
(1/3)(`m`²(3`n`-`m`) - (`m`-nfact)²(3`n` - 2nfact - `m`))	If `nfact < m < n`

The number of operations for complex flavors is four times greater.

When incomplete factorization is specified, the first nfact rows and columns are factored, with the update of the remaining rows and columns of A as follows:

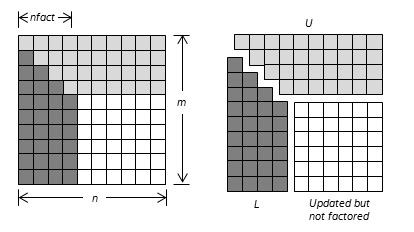
If matrix A is represented as a block 2-by-2 matrix:

where

A₁₁ is a square matrix of order nfact,
A₂₁ is an (m - nfact)-by-nfact matrix,
A₁₂ is an nfact-by-(n - nfact) matrix, and
A₂₂ is an (m - nfact)-by-(n - nfact) matrix.

The result is

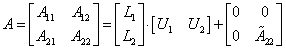
L₁ is a lower triangular square matrix of order nfact with unit diagonal and U₁ is an upper triangular square matrix of order nfact. L₁ and U₁ result from LU factorization of matrix A₁₁: A₁₁ = L₁U₁.

L₂ is an (m - nfact)-by-nfact matrix and L₂ = A₂₁U₁^-1. U₂ is an nfact-by-(n - nfact) matrix and U₂ = L₁^-1A₁₂.

is an (m - nfact)-by-(n - nfact) matrix and = A₂₂ - L₂U₂.

On exit, elements of the upper triangle U₁ are stored in place of the upper triangle of block A₁₁ in array a; elements of the lower triangle L₁ are stored in the lower triangle of block A₁₁ in array a (unit diagonal elements are not stored). Elements of L₂ replace elements of A₂₁; U₂ replaces elements of A₁₂ and replaces elements of A₂₂.

Parent topic: Matrix Factorization: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

mkl_?getrfnpi

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes