?pbstf

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 3/22/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-9CD5CAD1-BECB-45C9-A917-F258038E127E

View Details

?pbstf

Computes a split Cholesky factorization of a real symmetric or complex Hermitian positive-definite banded matrix used in ?sbgst/?hbgst .

Syntax

lapack_int LAPACKE_spbstf (int matrix_layout, char uplo, lapack_int n, lapack_int kb, float* bb, lapack_int ldbb);

lapack_int LAPACKE_dpbstf (int matrix_layout, char uplo, lapack_int n, lapack_int kb, double* bb, lapack_int ldbb);

lapack_int LAPACKE_cpbstf (int matrix_layout, char uplo, lapack_int n, lapack_int kb, lapack_complex_float* bb, lapack_int ldbb);

lapack_int LAPACKE_zpbstf (int matrix_layout, char uplo, lapack_int n, lapack_int kb, lapack_complex_double* bb, lapack_int ldbb);

Include Files

mkl.h

Description

The routine computes a split Cholesky factorization of a real symmetric or complex Hermitian positive-definite band matrix B. It is to be used in conjunction with sbgst/hbgst.

The factorization has the form B = S^T*S (or B = S^H*S for complex flavors), where S is a band matrix of the same bandwidth as B and the following structure: S is upper triangular in the first (n+kb)/2 rows and lower triangular in the remaining rows.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

uplo

Must be 'U' or 'L'.

If uplo = 'U', bb stores the upper triangular part of B.

If uplo = 'L', bb stores the lower triangular part of B.

n

The order of the matrix B (n≥ 0).

kb

The number of super- or sub-diagonals in B

(kb≥ 0).

bb

bb(size at least max(1, ldbb*n) for column major layout and at least max(1, ldbb*(kb + 1)) for row major layout) is an array containing either upper or lower triangular part of the matrix B (as specified by uplo) in band storage format.

ldbb

The leading dimension of bb; must be at least kb+1for column major and at least max(1, n) for row major.

Output Parameters

bb: On exit, this array is overwritten by the elements of the split Cholesky factor S.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = i, then the factorization could not be completed, because the updated element b_ii would be the square root of a negative number; hence the matrix B is not positive-definite.

If info = -i, the i-th parameter had an illegal value.

Application Notes

The computed factor S is the exact factor of a perturbed matrix B + E, where

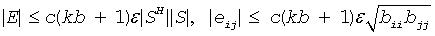
c(n) is a modest linear function of n, and ε is the machine precision.

The total number of floating-point operations for real flavors is approximately n(kb+1)². The number of operations for complex flavors is 4 times greater. All these estimates assume that kb is much less than n.

After calling this routine, you can call sbgst/hbgst to solve the generalized eigenproblem Az = λBz, where A and B are banded and B is positive-definite.

Parent topic: Generalized Symmetric-Definite Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?pbstf

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes