?tprfb

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 3/22/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-FF48933C-543E-49A5-9FB4-7AC111AFCE2B

View Details

?tprfb

Applies a real or complex "triangular-pentagonal" blocked reflector to a real or complex matrix, which is composed of two blocks.

Syntax

lapack_int LAPACKE_stprfb (int matrix_layout, char side, char trans, char direct, char storev, lapack_int m, lapack_int n, lapack_int k, lapack_int l, const float * v, lapack_int ldv, const float * t, lapack_int ldt, float * a, lapack_int lda, float * b, lapack_int ldb);

lapack_int LAPACKE_dtprfb (int matrix_layout, char side, char trans, char direct, char storev, lapack_int m, lapack_int n, lapack_int k, lapack_int l, const double * v, lapack_int ldv, const double * t, lapack_int ldt, double * a, lapack_int lda, double * b, lapack_int ldb);

lapack_int LAPACKE_ctprfb (int matrix_layout, char side, char trans, char direct, char storev, lapack_int m, lapack_int n, lapack_int k, lapack_int l, const lapack_complex_float * v, lapack_int ldv, const lapack_complex_float * t, lapack_int ldt, lapack_complex_float * a, lapack_int lda, lapack_complex_float * b, lapack_int ldb);

lapack_int LAPACKE_ztprfb (int matrix_layout, char side, char trans, char direct, char storev, lapack_int m, lapack_int n, lapack_int k, lapack_int l, const lapack_complex_double * v, lapack_int ldv, const lapack_complex_double * t, lapack_int ldt, lapack_complex_double * a, lapack_int lda, lapack_complex_double * b, lapack_int ldb);

Include Files

mkl.h

Description

The ?tprfb routine applies a real or complex "triangular-pentagonal" block reflector H, H^T, or H^H from either the left or the right to a real or complex matrix C, which is composed of two blocks A and B.

The block B is m-by-n. If side = 'R', A is m-by-k, and if side = 'L', A is of size k-by-n.

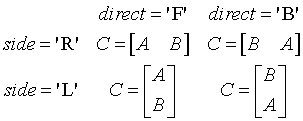
The pentagonal matrix V is composed of a rectangular block V1 and a trapezoidal block V2. The size of the trapezoidal block is determined by the parameter l, where 0≤l≤k. if l=k, the V2 block of V is triangular; if l=0, there is no trapezoidal block, thus V = V1 is rectangular.

	direct='F'	direct='B'
storev='C'	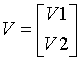`V2` is upper trapezoidal (first l rows of k-by-k upper triangular)	`V2` is lower trapezoidal (last l rows of k-by-k lower triangular matrix)
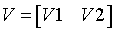
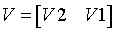
storev='R'	`V2` is lower trapezoidal (first l columns of k-by-k lower triangular matrix)	`V2` is upper trapezoidal (last l columns of k-by-k upper triangular matrix)

side='L'

side='R'

storev='C'

V is m-by-k

V2 is l-by-k

V is n-by-k

V2 is l-by-k

storev='R'

V is k-by-m

V2 is k-by-l

V is k-by-n

V2 is k-by-l

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major ( LAPACK_COL_MAJOR ).

side

= 'L': apply H, H^T, or H^H from the left,

= 'R': apply H, H^T, or H^H from the right.

trans

= 'N': apply H (no transpose),

= 'T': apply H^T (transpose),

= 'C': apply H^H (conjugate transpose).

direct

Indicates how H is formed from a product of elementary reflectors:

= 'F': H = H(1) H(2) . . . H(k) (Forward),

= 'B': H = H(k) . . . H(2) H(1) (Backward).

storev

Indicates how the vectors that define the elementary reflectors are stored:

= 'C': Columns,

= 'R': Rows.

m

The total number of rows in the matrix B (m ≥ 0).

n

The number of columns in B (n ≥ 0).

k

The order of the matrix T, which is the number of elementary reflectors whose product defines the block reflector. (k ≥ 0)

l

The order of the trapezoidal part of V. (k ≥ l ≥ 0).

v

An array containing the pentagonal matrix V (the elementary reflectors H(1), H(2), …, H(k). The size limitations depend on values of parameters storev and side as described in the following table

	`storev` = C		`storev` = R
	`side` = L	`side` = R	`side` = L	`side` = R
Column major	max(1,`ldv`*`k`)	max(1,`ldv`*`k`)	max(1,`ldv`*`m`)	max(1,`ldv`*`n`)
Row major	max(1,`ldv`*`m`)	max(1,`ldv`*`n`)	max(1,`ldv`*`k`)	max(1,`ldv`*`k`)

ldv

The leading dimension of the array v.It should satisfy the following conditions:

	`storev` = C		`storev` = R
	`side` = L	`side` = R	`side` = L	`side` = R
Column major	max(1,`m`)	max(1,`n`)	max(1,`k`)	max(1,`k`)
Row major	max(1,`k`)	max(1,`k`)	max(1,`m`)	max(1,`n`)

t

Array size max(1,ldt * k). The triangular k-by-k matrix T in the representation of the block reflector.

ldt

The leading dimension of the array t (ldt ≥ k).

a

size should satisfy the following conditions:

k if side = 'R'.

	`side` = L	`side` = R
Column major	max(1,`lda`*`n`)	max(1,`lda`*`k`)
Row major	max(1,`lda`*`k`)	max(1,`lda`*`m`)

The k-by-n or m-by-k matrix A.

lda

The leading dimension of the array a should satisfy the following conditions:

	`side` = L	`side` = R
Column major	max(1,`k`)	max(1,`m`)
Row major	max(1,`n`)	max(1,`k`)

b

Array size at least max(1, ldb *n) for column major layout and max(1, ldb *m) for row major layout, the m-by-n matrix B.

ldb

The leading dimension of the array b (ldb ≥ max(1, m) for column major layout and ldb ≥ max(1, n) for row major layout).

Output Parameters

a: Contains the corresponding block of H*C, H^T*C, H^H*C, C*H, C*H^T, or C*H^H.
b: Contains the corresponding block of H*C, H^T*C, H^H*C, C*H, C*H^T, or C*H^H.

Return Values

This function returns a value info.

If info = 0, the execution is successful.

If info < 0, the i-th parameter had an illegal value.

If info = -1011, memory allocation error occurred.

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?tprfb

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values