p?pocon

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 3/22/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-CBE6172F-6389-47EE-B61C-5D1B29D74E60

View Details

p?pocon

Estimates the reciprocal of the condition number (in the 1 - norm) of a symmetric / Hermitian positive-definite distributed matrix.

Syntax

void pspocon (char *uplo , MKL_INT *n , float *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , float *anorm , float *rcond , float *work , MKL_INT *lwork , MKL_INT *iwork , MKL_INT *liwork , MKL_INT *info );

void pdpocon (char *uplo , MKL_INT *n , double *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , double *anorm , double *rcond , double *work , MKL_INT *lwork , MKL_INT *iwork , MKL_INT *liwork , MKL_INT *info );

void pcpocon (char *uplo , MKL_INT *n , MKL_Complex8 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , float *anorm , float *rcond , MKL_Complex8 *work , MKL_INT *lwork , float *rwork , MKL_INT *lrwork , MKL_INT *info );

void pzpocon (char *uplo , MKL_INT *n , MKL_Complex16 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , double *anorm , double *rcond , MKL_Complex16 *work , MKL_INT *lwork , double *rwork , MKL_INT *lrwork , MKL_INT *info );

Include Files

mkl_scalapack.h

Description

The p?poconfunction estimates the reciprocal of the condition number (in the 1 - norm) of a real symmetric or complex Hermitian positive definite distributed matrix sub(A) = A(ia:ia+n-1, ja:ja+n-1), using the Cholesky factorization sub(A) = U^H*U or sub(A) = L*L^H computed by p?potrf.

An estimate is obtained for ||(sub(A))^-1||, and the reciprocal of the condition number is computed as

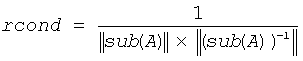
Input Parameters

uplo

(global) Must be 'U' or 'L'.

Specifies whether the factor stored in sub(A) is upper or lower triangular.

If uplo = 'U', sub(A) stores the upper triangular factor U of the Cholesky factorization sub(A) = U^H*U.

If uplo = 'L', sub(A) stores the lower triangular factor L of the Cholesky factorization sub(A) = L*L^H.

n

(global) The order of the distributed matrix sub(A) (n≥0).

a

(local)

Pointer into the local memory to an array of size lld_a*LOCc(ja+n-1).

The array a contains the local pieces of the factors L or U from the Cholesky factorization sub(A) = U^H*U, or sub(A) = L*L^H, as computed by p?potrf.

ia, ja

(global) The row and column indices in the global matrix A indicating the first row and the first column of the matrix sub(A), respectively.

desca

(global and local) array of size dlen_. The array descriptor for the distributed matrix A.

anorm

(global)

The 1-norm of the symmetric/Hermitian distributed matrix sub(A).

work

(local)

The array work of size lwork is a workspace array.

lwork

(local or global) The size of the array work.

For real flavors:

lwork must be at least

lwork≥ 2*LOCr(n+mod(ia-1,mb_a))+2*LOCc(n+mod(ja-1,nb_a))+max(2, max(nb_a*iceil(NPROW-1, NPCOL), LOCc(n+mod(ja-1,nb_a))+nb_a*iceil(NPCOL-1, NPROW))).

For complex flavors:

lwork must be at least

lwork≥ 2*LOCr(n+mod(ia-1,mb_a))+max(2, max(nb_a*max(1,iceil(NPROW-1, NPCOL)), LOCc(n+mod(ja-1,nb_a))+nb_a*max(1,iceil(NPCOL-1, NPROW)))).

If lwork = -1, then lwork is a global input and a workspace query is assumed. The routine only calculates the minimum and optimal size for all work arrays. Each value is returned in the first entry of the corresponding work array, and no error message is issued by pxerbla.

NOTE:

iceil(x,y) is the ceiling of x/y, and mod(x,y) is the integer remainder of x/y.

iwork

(local) Workspace array of size liwork. Used in real flavors only.

liwork

(local or global) The size of the array iwork; used in real flavors only. Must be at least liwork≥LOCr(n+mod(ia-1,mb_a)).

If liwork = -1, then liwork is a global input and a workspace query is assumed. The routine only calculates the minimum and optimal size for all work arrays. Each value is returned in the first entry of the corresponding work array, and no error message is issued by pxerbla.

rwork

(local)

Workspace array of size lrwork. Used in complex flavors only.

lrwork

(local or global) The size of the array rwork; used in complex flavors only. Must be at least lrwork≥ 2*LOCc(n+mod(ja-1,nb_a)).

If lrwork = -1, then lrwork is a global input and a workspace query is assumed. The routine only calculates the minimum and optimal size for all work arrays. Each value is returned in the first entry of the corresponding work array, and no error message is issued by pxerbla.

Output Parameters

rcond

(global)

The reciprocal of the condition number of the distributed matrix sub(A).

work[0]

On exit, work[0] contains the minimum value of lwork required for optimum performance.

iwork[0]

On exit, iwork[0] contains the minimum value of liwork required for optimum performance (for real flavors).

rwork[0]

On exit, rwork[0] contains the minimum value of lrwork required for optimum performance (for complex flavors).

info

(global) If info=0, the execution is successful.

info < 0:

If the i-th argument is an array and the j-th entry, indexed j - 1, had an illegal value, then info = -(i*100+j); if the i-th argument is a scalar and had an illegal value, then info = -i.

Parent topic: Estimating the Condition Number: ScaLAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

p?pocon

Syntax

Include Files

Description

Input Parameters

Output Parameters

See Also