?sptrs

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 3/22/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-29A1B330-50B2-4792-8BC6-CD372D185EEB

View Details

?sptrs

Solves a system of linear equations with a UDU- or LDL-factored symmetric coefficient matrix using packed storage.

Syntax

lapack_int LAPACKE_ssptrs (int matrix_layout , char uplo , lapack_int n , lapack_int nrhs , const float * ap , const lapack_int * ipiv , float * b , lapack_int ldb );

lapack_int LAPACKE_dsptrs (int matrix_layout , char uplo , lapack_int n , lapack_int nrhs , const double * ap , const lapack_int * ipiv , double * b , lapack_int ldb );

lapack_int LAPACKE_csptrs (int matrix_layout , char uplo , lapack_int n , lapack_int nrhs , const lapack_complex_float * ap , const lapack_int * ipiv , lapack_complex_float * b , lapack_int ldb );

lapack_int LAPACKE_zsptrs (int matrix_layout , char uplo , lapack_int n , lapack_int nrhs , const lapack_complex_double * ap , const lapack_int * ipiv , lapack_complex_double * b , lapack_int ldb );

Include Files

mkl.h

Description

The routine solves for X the system of linear equations A*X = B with a symmetric matrix A, given the Bunch-Kaufman factorization of A:

if `uplo='U'`,	`A` = `UDU^T`
if `uplo='L'`,	`A` = `LDL^T`,

where U and L are upper and lower packed triangular matrices with unit diagonal and D is a symmetric block-diagonal matrix. The system is solved with multiple right-hand sides stored in the columns of the matrix B. You must supply the factor U (or L) and the array ipiv returned by the factorization routine ?sptrf.

Input Parameters

matrix_layout	Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).
uplo	Must be 'U' or 'L'. Indicates how the input matrix `A` has been factored: If `uplo = 'U'`, the array `ap` stores the packed factor `U` of the factorization `A` = `UDU^T`. If `uplo = 'L'`, the array `ap` stores the packed factor `L` of the factorization `A` = `LDL^T`.
n	The order of matrix `A`; `n`≥ 0.
nrhs	The number of right-hand sides; `nrhs`≥ 0.
ipiv	Array, size at least `max(1, n)`. The `ipiv` array, as returned by ?sptrf.
ap	The dimension of array `ap` must be at least max(1, `n`(`n`+1)/2). The array `ap` contains the factor `U` or `L`, as specified by `uplo`, in packed storage (see Matrix Storage Schemes).
b	The array `b` contains the matrix `B` whose columns are the right-hand sides for the system of equations. The size of b is max(1, ldbnrhs) for column major layout and max(1, ldbn) for row major layout.
ldb	The leading dimension of `b`; `ldb`≥ max(1, n) for column major layout and `ldb`≥nrhs for row major layout.

Output Parameters

b	Overwritten by the solution matrix `X`.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, parameter i had an illegal value.

Application Notes

For each right-hand side b, the computed solution is the exact solution of a perturbed system of equations (A + E)x = b, where

|E| ≤ c(n)ε P|U||D||U^T|P^T or |E| ≤ c(n)ε P|L||D||L^T|P^T

c(n) is a modest linear function of n, and ε is the machine precision.

If x₀ is the true solution, the computed solution x satisfies this error bound:

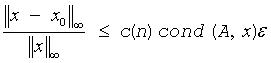
where cond(A,x)= || |A^-1||A| |x| ||_∞ / ||x||_∞≤ ||A^-1||_∞ ||A||_∞ = κ_∞(A).

Note that cond(A,x) can be much smaller than κ_∞(A).

The total number of floating-point operations for one right-hand side vector is approximately 2n² for real flavors or 8n² for complex flavors.

To estimate the condition number κ_∞(A), call ?spcon.

To refine the solution and estimate the error, call ?sprfs.

Parent topic: Solving Systems of Linear Equations: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?sptrs

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes

See Also