?gglse

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 3/22/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-0A5E0425-CE2C-41F0-BE4B-DE3EF043A0A1

View Details

?gglse

Solves the linear equality-constrained least squares problem using a generalized RQ factorization.

Syntax

lapack_int LAPACKE_sgglse (int matrix_layout, lapack_int m, lapack_int n, lapack_int p, float* a, lapack_int lda, float* b, lapack_int ldb, float* c, float* d, float* x);

lapack_int LAPACKE_dgglse (int matrix_layout, lapack_int m, lapack_int n, lapack_int p, double* a, lapack_int lda, double* b, lapack_int ldb, double* c, double* d, double* x);

lapack_int LAPACKE_cgglse (int matrix_layout, lapack_int m, lapack_int n, lapack_int p, lapack_complex_float* a, lapack_int lda, lapack_complex_float* b, lapack_int ldb, lapack_complex_float* c, lapack_complex_float* d, lapack_complex_float* x);

lapack_int LAPACKE_zgglse (int matrix_layout, lapack_int m, lapack_int n, lapack_int p, lapack_complex_double* a, lapack_int lda, lapack_complex_double* b, lapack_int ldb, lapack_complex_double* c, lapack_complex_double* d, lapack_complex_double* x);

Include Files

mkl.h

Description

The routine solves the linear equality-constrained least squares (LSE) problem:

minimize ||c - A*x||² subject to B*x = d

where A is an m-by-n matrix, B is a p-by-n matrix, c is a given m-vector, andd is a given p-vector. It is assumed that p≤n≤m+p, and

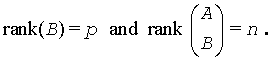
These conditions ensure that the LSE problem has a unique solution, which is obtained using a generalized RQ factorization of the matrices (B, A) given by

B=(0 R)*Q, A=Z*T*Q

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

m

The number of rows of the matrix A (m≥ 0).

n

The number of columns of the matrices A and B (n≥ 0).

p

The number of rows of the matrix B

(0 ≤p≤n≤m+p).

a, b, c, d

Arrays:

a(size max(1, lda*n) for column major layout and max(1, lda*m) for row major layout) contains the m-by-n matrix A.

b(size max(1, ldb*n) for column major layout and max(1, ldb*p) for row major layout) contains the p-by-nmatrix B.

c size at least max(1, m), contains the right hand side vector for the least squares part of the LSE problem.

d, size at least max(1, p), contains the right hand side vector for the constrained equation.

lda

The leading dimension of a; at least max(1, m)for column major layout and max(1, n) for row major layout.

ldb

The leading dimension of b; at least max(1, p)for column major layout and max(1, n) for row major layout.

Output Parameters

a: The elements on and above the diagonal contain the min(m, n)-by-n upper trapezoidal matrix T as returned by ?ggrqf.
x: The solution of the LSE problem.
b: On exit, the upper right triangle contains the p-by-p upper triangular matrix R as returned by ?ggrqf.
d: On exit, d is destroyed.
c: On exit, the residual sum-of-squares for the solution is given by the sum of squares of elements n-p+1 to m of vector c.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = 1, the upper triangular factor R associated with B in the generalized RQ factorization of the pair (B, A) is singular, so that rank(B) < p; the least squares solution could not be computed.

If info = 2, the (n-p)-by-(n-p) part of the upper trapezoidal factor T associated with A in the generalized RQ factorization of the pair (B, A) is singular, so that

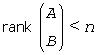
; the least squares solution could not be computed.

Parent topic: Generalized Linear Least Squares (LLS) Problems: LAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?gglse

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values