?tpqrt

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-4E76B45F-A4E9-4282-BA5E-463F6FD28B56

View Details

?tpqrt

Computes a blocked QR factorization of a real or complex "triangular-pentagonal" matrix, which is composed of a triangular block and a pentagonal block, using the compact WY representation for Q.

Syntax

call stpqrt(m, n, l, nb, a, lda, b, ldb, t, ldt, work, info)

call dtpqrt(m, n, l, nb, a, lda, b, ldb, t, ldt, work, info)

call ctpqrt(m, n, l, nb, a, lda, b, ldb, t, ldt, work, info)

call ztpqrt(m, n, l, nb, a, lda, b, ldb, t, ldt, work, info)

call tpqrt(a, b, t, nb[, info])

Include Files

mkl.fi, lapack.f90

Description

The input matrix C is an (n+m)-by-n matrix

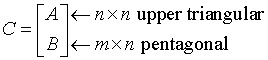
where A is an n-by-n upper triangular matrix, and B is an m-by-n pentagonal matrix consisting of an (m-l)-by-n rectangular matrix B1 on top of an l-by-n upper trapezoidal matrix B2:

The upper trapezoidal matrix B2 consists of the first l rows of an n-by-n upper triangular matrix, where 0 ≤ l ≤ min(m,n). If l=0, B is an m-by-n rectangular matrix. If m=l=n, B is upper triangular. The elementary reflectors H(i) are stored in the ith column below the diagonal in the (n+m)-by-n input matrix C. The structure of vectors defining the elementary reflectors is illustrated by:

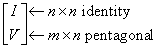
The elements of the unit matrix I are not stored. Thus, V contains all of the necessary information, and is returned in array b.

NOTE:

Note that V has the same form as B:

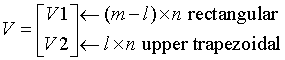
The columns of V represent the vectors which define the H(i)s.

The number of blocks is k = ceiling(n/nb), where each block is of order nb except for the last block, which is of order ib = n - (k-1)*nb. For each of the k blocks, an upper triangular block reflector factor is computed: T1, T2, ..., Tk. The nb-by-nb (ib-by-ib for the last block) Tis are stored in the nb-by-n array t as

t = [T1T2 ... Tk] .

Input Parameters

m

INTEGER. The total number of rows in the matrix B (m ≥ 0).

n

INTEGER. The number of columns in B and the order of the triangular matrix A (n ≥ 0).

l

INTEGER. The number of rows of the upper trapezoidal part of B (min(m, n) ≥ l ≥ 0).

nb

INTEGER. The block size to use in the blocked QR factorization (n ≥ nb ≥ 1).

a, b, work

REAL for stpqrt

DOUBLE PRECISION for dtpqrt

COMPLEX for ctpqrt

COMPLEX*16 for ztpqrt.

Arrays: a size (lda, n) contains the n-by-n upper triangular matrix A.

b size (ldb, n), the pentagonal m-by-n matrix B. The first (m-l) rows contain the rectangular B1 matrix, and the next l rows contain the upper trapezoidal B2 matrix.

work size (nb, n) is a workspace array.

lda

INTEGER. The leading dimension of a; at least max(1, n).

ldb

INTEGER. The leading dimension of b; at least max(1, m).

ldt

INTEGER. The leading dimension of t; at least nb.

Output Parameters

a

The elements on and above the diagonal of the array contain the upper triangular matrix R.

b

The pentagonal matrix V.

t

REAL for stpqrt

DOUBLE PRECISION for dtpqrt

COMPLEX for ctpqrt

COMPLEX*16 for ztpqrt.

Array, size (ldt, n).

The upper triangular block reflectors stored in compact form as a sequence of upper triangular blocks.

info

INTEGER.

If info = 0, the execution is successful.

If info < 0 and info = -i, the ith argument had an illegal value.

Parent topic: Orthogonal Factorizations: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?tpqrt

Syntax

Include Files

Description

Input Parameters

Output Parameters