?potrf2

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-11BCB871-887C-4F29-9500-863F83DF6B41

View Details

?potrf2

Computes Cholesky factorization using a recursive algorithm.

Syntax

call spotrf2(uplo, n, a, lda, info)

call dpotrf2(uplo, n, a, lda, info)

call cpotrf2(uplo, n, a, lda, info)

call zpotrf2(uplo, n, a, lda, info)

Include Files

mkl.fi

Description

?potrf2 computes the Cholesky factorization of a real or complex symmetric positive definite matrix A using the recursive algorithm.

The factorization has the form

for real flavors:

A = U^T * U, if uplo = 'U', or

A = L * L^T, if uplo = 'L',

for complex flavors:

A = U^H * U, if uplo = 'U',

or A = L * L^H, if uplo = 'L',

where U is an upper triangular matrix and L is lower triangular.

This is the recursive version of the algorithm. It divides the matrix into four submatrices:

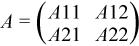
where A11 is n1 by n1 and A22 is n2 by n2, with n1 = n/2 and n2 = n-n1.

The subroutine calls itself to factor A11. Update and scale A21 or A12, update A22 then call itself to factor A22.

Input Parameters

uplo

CHARACTER*1. = 'U': Upper triangle of A is stored;

= 'L': Lower triangle of A is stored.

n

INTEGER. The order of the matrix A.

n≥ 0.

a

REAL for spotrf2

DOUBLE PRECISION for dpotrf2

COMPLEX for cpotrf2

DOUBLE COMPLEX for zpotrf2

Array, size (lda, n).

On entry, the symmetric matrix A.

If uplo = 'U', the leading n-by-n upper triangular part of a contains the upper triangular part of the matrix A, and the strictly lower triangular part of a is not referenced.

If uplo = 'L', the leading n-by-n lower triangular part of a contains the lower triangular part of the matrix A, and the strictly upper triangular part of a is not referenced.

lda

INTEGER. The leading dimension of the array a.

lda≥ max(1,n).

Output Parameters

On exit, if info = 0, the factor U or L from the Cholesky factorization.

For real flavors:

A = U^T*U or A = L*L^T;

For complex flavors:

A = U^H*U or A = L*L^H.

info

INTEGER. = 0: successful exit

< 0: if info = -i, the i-th argument had an illegal value

> 0: if info = i, the leading minor of order i is not positive definite, and the factorization could not be completed.

Parent topic: Matrix Factorization: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?potrf2

Syntax

Include Files

Description

Input Parameters

Output Parameters