?gbtrf

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-03E2AA41-0886-485D-B0D7-1C2186119220

View Details

?gbtrf

Computes the LU factorization of a general m-by-n band matrix.

Syntax

call sgbtrf( m, n, kl, ku, ab, ldab, ipiv, info )

call dgbtrf( m, n, kl, ku, ab, ldab, ipiv, info )

call cgbtrf( m, n, kl, ku, ab, ldab, ipiv, info )

call zgbtrf( m, n, kl, ku, ab, ldab, ipiv, info )

call gbtrf( ab [,kl] [,m] [,ipiv] [,info] )

Include Files

mkl.fi, lapack.f90

Description

The routine forms the LU factorization of a general m-by-n band matrix A with kl non-zero subdiagonals and ku non-zero superdiagonals, that is,

A = P*L*U,

where P is a permutation matrix; L is lower triangular with unit diagonal elements and at most kl non-zero elements in each column; U is an upper triangular band matrix with kl + ku superdiagonals. The routine uses partial pivoting, with row interchanges (which creates the additional kl superdiagonals in U).

NOTE:

This routine supports the Progress Routine feature. See Progress Function for details.

Input Parameters

m	INTEGER. The number of rows in matrix `A`; `m`≥ 0.
n	INTEGER. The number of columns in matrix `A`; `n`≥ 0.
kl	INTEGER. The number of subdiagonals within the band of `A`; `kl`≥ 0.
ku	INTEGER. The number of superdiagonals within the band of `A`; `ku`≥ 0.
ab	REAL for sgbtrf DOUBLE PRECISION for dgbtrf COMPLEX for cgbtrf DOUBLE COMPLEX for zgbtrf. Array, size `ldab` by . The array `ab` contains the matrix `A` in band storage, in rows `kl + 1` to `2kl + ku + 1`; rows 1 to `kl` of the array need not be set. The `j`-th column of `A` is stored in the `j`-th column of the array `ab` as follows: `ab(kl + ku + 1 + i - j, j) = a(i,j)` for `max(1,j-ku) ≤i≤ min(m,j+kl)`.
ldab	INTEGER. The leading dimension of the array `ab`. (`ldab`≥ 2*`kl` + `ku` + 1)

Output Parameters

Overwritten by L and U. U is stored as an upper triangular band matrix with kl + ku superdiagonals in rows 1 to kl + ku + 1, and the multipliers used during the factorization are stored in rows kl + ku + 2 to 2*kl + ku + 1.

See Application Notes below for further details.

ipiv

INTEGER.

Array, size at least max(1,min(m, n)). The pivot indices; for 1 ≤i≤ min(m, n) , row i was interchanged with row ipiv(i).

info

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = i, u_iiis 0. The factorization has been completed, but U is exactly singular. Division by 0 will occur if you use the factor U for solving a system of linear equations.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or reconstructible arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine gbtrf interface are as follows:

ab	Holds the array `A` of size (`2*kl+ku+1,n`).
ipiv	Holds the vector of length `min(m,n)`.
kl	If omitted, assumed `kl = ku`.
ku	Restored as `ku = lda-2*kl-1`.
m	If omitted, assumed `m = n`.

Application Notes

The computed L and U are the exact factors of a perturbed matrix A + E, where

|E| ≤ c(kl+ku+1) ε P|L||U|

c(k) is a modest linear function of k, and ε is the machine precision.

The total number of floating-point operations for real flavors varies between approximately 2n(ku+1)kl and 2n(kl+ku+1)kl. The number of operations for complex flavors is four times greater. All these estimates assume that kl and ku are much less than min(m,n).

The band storage scheme is illustrated by the following example, when m = n = 6, kl = 2, ku = 1:

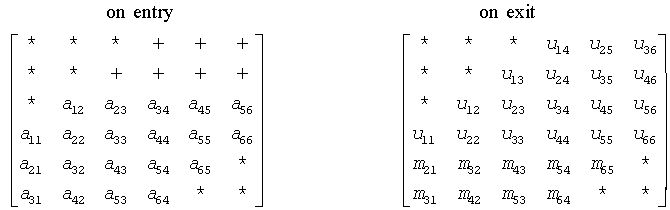
Elements marked * are not used; elements marked + need not be set on entry, but are required by the routine to store elements of U because of fill-in resulting from the row interchanges.

After calling this routine with m = n, you can call the following routines:

gbtrs	to solve `AX = B` or `A^TX = B` or `A^H*X = B`
gbcon	to estimate the condition number of `A`.

Parent topic: Matrix Factorization: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?gbtrf

Syntax

Include Files

Description

Input Parameters

Output Parameters

LAPACK 95 Interface Notes

Application Notes

See Also