?tpmqrt

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-46CC24AC-BDE1-498A-9413-BFB82BEA60E8

View Details

?tpmqrt

Applies a real or complex orthogonal matrix obtained from a "triangular-pentagonal" complex block reflector to a general real or complex matrix, which consists of two blocks.

Syntax

call stpmqrt(side, trans, m, n, k, l, nb, v, ldv, t, ldt, a, lda, b, ldb, work, info)

call dtpmqrt(side, trans, m, n, k, l, nb, v, ldv, t, ldt, a, lda, b, ldb, work, info)

call ctpmqrt(side, trans, m, n, k, l, nb, v, ldv, t, ldt, a, lda, b, ldb, work, info)

call ztpmqrt(side, trans, m, n, k, l, nb, v, ldv, t, ldt, a, lda, b, ldb, work, info)

call tpmqrt( v, t, a, b, k, nb[, trans][, side][, info])

Include Files

mkl.fi, lapack.f90

Description

The columns of the pentagonal matrix V contain the elementary reflectors H(1), H(2), ..., H(k); V is composed of a rectangular block V1 and a trapezoidal block V2:

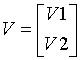
The size of the trapezoidal block V2 is determined by the parameter l, where 0 ≤ l ≤ k. V2 is upper trapezoidal, consisting of the first l rows of a k-by-k upper triangular matrix.

If l=k, V2 is upper triangular;

If l=0, there is no trapezoidal block, so V = V1 is rectangular.

If side = 'L':

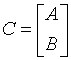
where A is k-by-n, B is m-by-n and V is m-by-k.

If side = 'R':

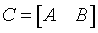
where A is m-by-k, B is m-by-n and V is n-by-k.

The real/complex orthogonal matrix Q is formed from V and T.

If trans='N' and side='L', c contains Q * C on exit.

If trans='T' and side='L', C contains Q^T * C on exit.

If trans='C' and side='L', C contains Q^H * C on exit.

If trans='N' and side='R', C contains C * Q on exit.

If trans='T' and side='R', C contains C * Q^T on exit.

If trans='C' and side='R', C contains C * Q^H on exit.

Input Parameters

side

CHARACTER*1

='L': apply Q, Q^T, or Q^H from the left.

='R': apply Q, Q^T, or Q^H from the right.

trans

CHARACTER*1

='N', no transpose, apply Q.

='T', transpose, apply Q^T.

='C', transpose, apply Q^H.

m

INTEGER. The number of rows in the matrix B, (m ≥ 0).

n

INTEGER. The number of columns in the matrix B, (n ≥ 0).

k

INTEGER. The number of elementary reflectors whose product defines the matrix Q, (k ≥ 0).

l

INTEGER. The order of the trapezoidal part of V (k ≥ l ≥ 0).

nb

INTEGER.

The block size used for the storage of t, k ≥ nb ≥ 1. This must be the same value of nb used to generate t in tpqrt.

v

REAL for stpmqrt

DOUBLE PRECISION for dtpmqrt

COMPLEX for ctpmqrt

COMPLEX*16 for ztpmqrt.

Size (ldv, k)

The ith column must contain the vector which defines the elementary reflector H(i), for i = 1,2,...,k, as returned by tpqrt in array argument b.

ldv

INTEGER. The leading dimension of the array v.

If side = 'L', ldv must be at least max(1,m);

If side = 'R', ldv must be at least max(1,n).

t

REAL for stpmqrt

DOUBLE PRECISION for dtpmqrt

COMPLEX for ctpmqrt

COMPLEX*16 for ztpmqrt.

Array, size (ldt, k).

The upper triangular factors of the block reflectors as returned by tpqrt, stored as an nb-by-k matrix.

ldt

INTEGER. The leading dimension of the array t. ldt must be at least nb.

a

REAL for stpmqrt

DOUBLE PRECISION for dtpmqrt

COMPLEX for ctpmqrt

COMPLEX*16 for ztpmqrt.

If side = 'L', size (lda, n).

If side = 'R', size (lda, k).

The k-by-n or m-by-k matrix A.

lda

INTEGER. The leading dimension of the array a.

If side = 'L', lda must be at least max(1,k).

If side = 'R', lda must be at least max(1,m).

b

REAL for stpmqrt

DOUBLE PRECISION for dtpmqrt

COMPLEX for ctpmqrt

COMPLEX*16 for ztpmqrt.

Size (ldb, n).

The m-by-n matrix B.

ldb

INTEGER. The leading dimension of the array b. ldb must be at least max(1,m).

work

REAL for stpmqrt

DOUBLE PRECISION for dtpmqrt

COMPLEX for ctpmqrt

COMPLEX*16 for ztpmqrt.

Workspace array. If side = 'L' DIMENSION n*nb. If side = 'R' DIMENSION m*nb.

Output Parameters

a

Overwritten by the corresponding block of the product Q*C, C*Q, Q^T*C, C*Q^T, Q^H*C, or C*Q^H.

b

Overwritten by the corresponding block of the product Q*C, C*Q, Q^T*C, C*Q^T, Q^H*C, or C*Q^H.

info

(global) INTEGER.

= 0: the execution is successful.

< 0: if info = -i, the ith argument had an illegal value.

Parent topic: Orthogonal Factorizations: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?tpmqrt

Syntax

Include Files

Description

Input Parameters

Output Parameters