?bdsvdx

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-9ED7B9A9-E7F8-462B-88FE-01F364BFC8D1

View Details

?bdsvdx

Computes the SVD of a bidiagonal matrix.

Syntax

call sbdsvdx (uplo, jobz, range, n, d, e, vl, vu, il, iu, ns, s, z, ldz, work, iwork, info )

call dbdsvdx (uplo, jobz, range, n, d, e, vl, vu, il, iu, ns, s, z, ldz, work, iwork, info )

Include Files

mkl.fi

Description

?bdsvdx computes the singular value decomposition (SVD) of a real n-by-n (upper or lower) bidiagonal matrix B, B = U * S * VT, where S is a diagonal matrix with non-negative diagonal elements (the singular values of B), and U and VT are orthogonal matrices of left and right singular vectors, respectively.

Given an upper bidiagonal B with diagonal d = [d₁d₂ ... d_n] and superdiagonal e = [e₁e₂ ... e_{n - 1}], ?bdsvdx computes the singular value decompositon of B through the eigenvalues and eigenvectors of the n*2-by-n*2 tridiagonal matrix

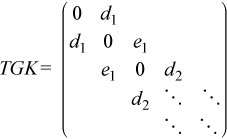
If (s,u,v) is a singular triplet of B with ||u|| = ||v|| = 1, then (±s,q), ||q|| = 1, are eigenpairs of TGK, with 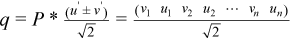, and .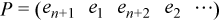

Given a TGK matrix, one can either

compute -s, -v and change signs so that the singular values (and corresponding vectors) are already in descending order (as in ?gesvd/?gesdd) or
compute s, v and reorder the values (and corresponding vectors).

?bdsvdx implements (1) by calling ?stevx (bisection plus inverse iteration, to be replaced with a version of the Multiple Relative Robust Representation algorithm. (See P. Willems and B. Lang, A framework for the MR^3 algorithm: theory and implementation, SIAM J. Sci. Comput., 35:740-766, 2013.)

Input Parameters

uplo

CHARACTER*1. = 'U': B is upper bidiagonal;

= 'L': B is lower bidiagonal.

jobz

CHARACTER*1. = 'N': Compute singular values only;

= 'V': Compute singular values and singular vectors.

range

CHARACTER*1. = 'A': Find all singular values.

= 'V': all singular values in the half-open interval [vl,vu) are found.

= 'I': the il-th through iu-th singular values are found.

n

INTEGER. The order of the bidiagonal matrix.

n >= 0.

d

REAL for sbdsvdx

DOUBLE PRECISION for dbdsvdx

Array, size n.

The n diagonal elements of the bidiagonal matrix B.

e

REAL for sbdsvdx

DOUBLE PRECISION for dbdsvdx

Array, size (max(1,n - 1))

The (n - 1) superdiagonal elements of the bidiagonal matrix B in elements 1 to n - 1.

vl

REAL for sbdsvdx

DOUBLE PRECISION for dbdsvdx

vl≥ 0.

vu

REAL for sbdsvdx

DOUBLE PRECISION for dbdsvdx

If range='V', the lower and upper bounds of the interval to be searched for singular values. vu > vl.

Not referenced if range = 'A' or 'I'.

il, iu

INTEGER. If range='I', the indices (in ascending order) of the smallest and largest singular values to be returned.

1 ≤il≤iu≤ min(m,n), if min(m,n) > 0.

Not referenced if range = 'A' or 'V'.

ldz

INTEGER. The leading dimension of the array z.

ldz≥ 1, and if jobz = 'V', ldz≥ max(2,n*2).

Output Parameters

ns	INTEGER. The total number of singular values found. 0 ≤ns≤n. If range = 'A', ns = n, and if range = 'I', ns = iu - il + 1.
s	REAL for sbdsvdx DOUBLE PRECISION for dbdsvdx Array, size (n) The first ns elements contain the selected singular values in ascending order.
z	REAL for sbdsvdx DOUBLE PRECISION for dbdsvdx Array, size (2n, `k`) If jobz = 'V', then if info = 0 the first ns columns of z contain the singular vectors of the matrix `B` corresponding to the selected singular values, with `U` in rows 1 to n and `V` in rows n+1 to n2, i.e. z = If jobz = 'N', then z is not referenced. NOTE: Make sure that at least `k` = ns+1 columns are supplied in the array z; if range = 'V', the exact value of ns is not known in advance and an upper bound must be used.
work	REAL for sbdsvdx DOUBLE PRECISION for dbdsvdx Array, size (14*n)
iwork	INTEGER. Array, size (12*n). If jobz = 'V', then if info = 0, the first ns elements of iwork are zero. If info > 0, then iwork contains the indices of the eigenvectors that failed to converge in ?stevx.
info	INTEGER. = 0: successful exit. < 0: if info = -`i`, the `i`-th argument had an illegal value. > 0: if info = `i`, then `i` eigenvectors failed to converge in ?stevx. The indices of the eigenvectors (as returned by ?stevx) are stored in the array iwork. if info = n*2 + 1, an internal error occurred.

Parent topic: Singular Value Decomposition: LAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?bdsvdx

Syntax

Include Files

Description

Input Parameters

Output Parameters