p?larft

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-B2F36D3E-02BB-4364-B30B-FA862B96C7B0

View Details

p?larft

Forms the triangular vector T of a block reflector H=I-V*T*V^H.

Syntax

call pslarft(direct, storev, n, k, v, iv, jv, descv, tau, t, work)

call pdlarft(direct, storev, n, k, v, iv, jv, descv, tau, t, work)

call pclarft(direct, storev, n, k, v, iv, jv, descv, tau, t, work)

call pzlarft(direct, storev, n, k, v, iv, jv, descv, tau, t, work)

Description

The p?larftroutine forms the triangular factor T of a real/complex block reflector H of order n, which is defined as a product of k elementary reflectors.

If direct = 'F', H = H(1)*H(2)...*H(k), and T is upper triangular;

If direct = 'B', H = H(k)*...*H(2)*H(1), and T is lower triangular.

If storev = 'C', the vector which defines the elementary reflector H(i) is stored in the i-th column of the distributed matrix V, and

H = I-V*T*V'

If storev = 'R', the vector which defines the elementary reflector H(i) is stored in the i-th row of the distributed matrix V, and

H = I-V'*T*V.

Input Parameters

direct

(global) CHARACTER*1.

Specifies the order in which the elementary reflectors are multiplied to form the block reflector:

if direct = 'F': H = H(1)*H(2)*...*H(k) (forward)

if direct = 'B': H = H(k)*...*H(2)*H(1) (backward).

storev

(global) CHARACTER*1.

Specifies how the vectors that define the elementary reflectors are stored (See Application Notes below):

if storev = 'C': columnwise;

if storev = 'R': rowwise.

n

(global) INTEGER.

The order of the block reflector H. n ≥ 0.

k

(global) INTEGER.

The order of the triangular factor T, is equal to the number of elementary reflectors.

1 ≤ k ≤ mb_v (= nb_v).

v

REAL for pslarft

DOUBLE PRECISION for pdlarft

COMPLEX for pclarft

COMPLEX*16 for pzlarft.

Pointer into the local memory to an array of local size

(LOCr(iv+n-1), LOCc(jv+k-1)) if storev = 'C', and

(LOCr(iv+k-1), LOCc(jv+n-1)) if storev = 'R'.

The distributed matrix V contains the Householder vectors. (See Application Notes below).

iv, jv

(global) INTEGER.

The row and column indices in the global matrix V indicating the first row and the first column of the matrix sub(V), respectively.

descv

(local) INTEGER array of size dlen_. The array descriptor for the distributed matrix V.

tau

(local)

REAL for pslarft

DOUBLE PRECISION for pdlarft

COMPLEX for pclarft

COMPLEX*16 for pzlarft.

Array of size LOCr(iv+k-1) if incv = m_v, and LOCc(jv+k-1) otherwise. This array contains the Householder scalars related to the Householder vectors.

tau is tied to the distributed matrix V.

work

(local).

REAL for pslarft

DOUBLE PRECISION for pdlarft

COMPLEX for pclarft

COMPLEX*16 for pzlarft.

Workspace array of size k*(k -1)/2.

Output Parameters

v

REAL for pslarft

DOUBLE PRECISION for pdlarft

COMPLEX for pclarft

COMPLEX*16 for pzlarft.

t

(local)

REAL for pslarft

DOUBLE PRECISION for pdlarft

COMPLEX for pclarft

COMPLEX*16 for pzlarft.

Array of size ( nb_v, nb_v) if storev = 'C', and ( mb_v, mb_v) otherwise. It contains the k-by-k triangular factor of the block reflector associated with v. If direct = 'F', t is upper triangular;

if direct = 'B', t is lower triangular.

Application Notes

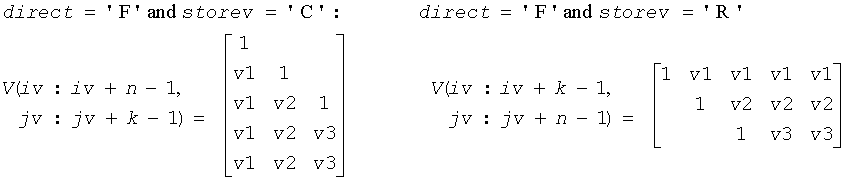
The shape of the matrix V and the storage of the vectors that define the H(i) is best illustrated by the following example with n = 5 and k = 3. The elements equal to 1 are not stored; the corresponding array elements are modified but restored on exit. The rest of the array is not used.