DFTI_PACKED

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-F65C2255-963E-429F-9E74-99DFBCE1526F

View Details

DFTI_PACKED_FORMAT

The result of the forward transform of real data is a conjugate-even sequence. Due to the symmetry property, only a part of the complex-valued sequence is stored in memory. The combination of the DFTI_PACKED_FORMAT and DFTI_CONJUGATE_EVEN_STORAGE configuration parameters defines how the conjugate-even sequence data is packed. If DFTI_CONJUGATE_EVEN_STORAGE is set to DFTI_COMPLEX_COMPLEX (default), the only possible value of DFTI_PACKED_FORMAT is DFTI_CCE_FORMAT; this association of configuration parameters is supported for transforms of any dimension. For a description of the corresponding packed format, see DFTI_CONJUGATE_EVEN_STORAGE. For one-dimensional transforms (only) with DFTI_CONJUGATE_EVEN_STORAGE set to DFTI_COMPLEX_REAL, the DFTI_PACKED_FORMAT configuration parameter must be DFTI_CCS_FORMAT, DFTI_PACK_FORMAT, or DFTI_PERM_FORMAT. The corresponding packed formats are explained and illustrated below.

DFTI_CCS_FORMAT for One-dimensional Transforms

The following figure illustrates the storage of a one-dimensional (1D) size-N conjugate-even sequence in a real array for the CCS, PACK, and PERM packed formats. The CCS format requires an array of size N+2, while the other formats require an array of size N. Zero-based indexing is used.

Storage of a 1D Size-N Conjugate-even Sequence in a Real Array

NOTE:

For storage of a one-dimensional conjugate-even sequence in a real array, CCS is in the same format as CCE.

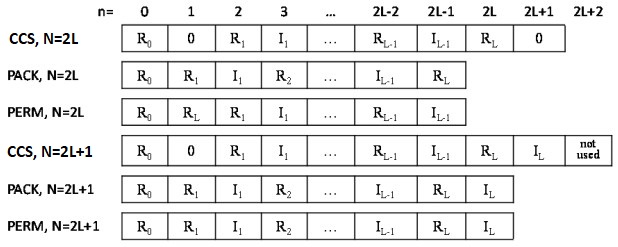
The real and imaginary parts of the complex-valued conjugate-even sequence Z_k are located in a real-valued array AC as illustrated by figure "Storage of a 1D Size-N Conjugate-even Sequence in a Real Array" and can be used to reconstruct the whole conjugate-even sequence as follows:

real :: AR(N), AC(N+2)
...
status = DftiSetValue( desc, DFTI_PACKED_FORMAT, DFTI_CCS_FORMAT )
...
! on input:  R{k} = AR(k)
status = DftiComputeForward( desc, AR, AC )  ! real-to-complex FFT
! on output:
! for k=1 … N/2+1: Z{k} = cmplx( AC(1 + (2*(k-1)+0)),
!                                AC(1 + (2*(k-1)+1)) )
! for k=N/2+2 … N: Z{k} = cmplx( AC(1 + (2*mod(N-k+1,N)+0)),
!                               -AC(1 + (2*mod(N-k+1,N)+1)))

DFTI_PACK_FORMAT for One-dimensional Transforms

real :: AR(N), AC(N)
...
status = DftiSetValue( desc, DFTI_PACKED_FORMAT, DFTI_PACK_FORMAT )
...
! on input:  R{k} = AR(k)
status = DftiComputeForward( desc, AR, AC )  ! real-to-complex FFT
! on output: Z{k} = cmplx( re, im ), where
!  if (k == 1) then
!    re =  AC(1)
!    im =  0
!  else if (k-1 == N-k+1) then
!    re =  AC(2*(k-1))
!    im =  0
!  else if (k <= N/2+1) then
!    re =  AC(2*(k-1)+0)
!    im =  AC(2*(k-1)+1)
!  else
!    re =  AC(2*(N-k+1)+0)
!    im = -AC(2*(N-k+1)+1)
!  end if

DFTI_PERM_FORMAT for One-dimensional Transforms

The real and imaginary parts of the complex-valued conjugate-even sequence Z_k are located in real-valued array AC as illustrated by figure "Storage of a 1D Size-N Conjugate-even Sequence in a Real Array" and can be used to reconstruct the whole conjugate-even sequence as follows:

real :: AR(N), AC(N)
...
status = DftiSetValue( desc, DFTI_PACKED_FORMAT, DFTI_PERM_FORMAT )
...
! on input:  R{k} = AR(k)
status = DftiComputeForward( desc, AR, AC )  ! real-to-complex FFT
! on output: Z{k} = cmplx( re, im ), where
! if (k == 1) then
!   re =  AC(1)
!   im =  0
! else if (k-1 == N-k+1) then
!   re =  AC(2)
!   im =  0
! else if (k <= N/2+1) then
!   re =  AC(1+2*(k-1)+0-mod(N,2))
!   im =  AC(1+2*(k-1)+1-mod(N,2))
! else
!   re =  AC(1+2*(N-k+1)+0-mod(N,2))
!   im = -AC(1+2*(N-k+1)+1-mod(N,2))
! end if

Parent topic: Configuration Settings

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

DFTI_PACKED_FORMAT

DFTI_CCS_FORMAT for One-dimensional Transforms

DFTI_PACK_FORMAT for One-dimensional Transforms

DFTI_PERM_FORMAT for One-dimensional Transforms

See Also