?feast_srci/?feast

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-FF098497-4F57-4253-9973-8547BE48FE0F

View Details

?feast_srci/?feast_hrci

Extended Eigensolver RCI interface.

Syntax

call sfeast_srci (ijob, n, ze, work, workc, aq, sq, fpm, epsout, loop, emin, emax, m0, lambda, q, m, res, info)

call dfeast_srci (ijob, n, ze, work, workc, aq, sq, fpm, epsout, loop, emin, emax, m0, lambda, q, m, res, info)

call cfeast_hrci (ijob, n, ze, work, workc, aq, sq, fpm, epsout, loop, emin, emax, m0, lambda, q, m, res, info)

call zfeast_hrci (ijob, n, ze, work, workc, aq, sq, fpm, epsout, loop, emin, emax, m0, lambda, q, m, res, info)

Include Files

mkl.fi

Description

Compute eigenvalues as described in Extended Eigensolver RCI Interface Description.

Input Parameters

ijob

INTEGER

Job indicator variable. On entry, a call to ?feast_srci/?feast_hrci with ijob=-1 initializes the eigensolver.

n

INTEGER

Sets the size of the problem. n > 0.

work

REAL for sfeast_srci

DOUBLE PRECISION for dfeast_srci

COMPLEX for cfeast_hrci

COMPLEX*16 for zfeast_hrci

Workspace array of size n by m0.

workc

COMPLEX for sfeast_srci and cfeast_hrci

COMPLEX*16 for dfeast_srci and zfeast_hrci

Workspace array of size n by m0.

aq, sq

REAL for sfeast_srci

DOUBLE PRECISION for dfeast_srci

COMPLEX for cfeast_hrci

COMPLEX*16 for zfeast_hrci

Workspace arrays of size m0 by m0.

fpm

INTEGER

Array, size of 128. This array is used to pass various parameters to Extended Eigensolver routines. See Extended Eigensolver Input Parameters for a complete description of the parameters and their default values.

emin, emax

REAL for sfeast_srci and cfeast_hrci

DOUBLE PRECISION for dfeast_srci and zfeast_hrci

The lower and upper bounds of the interval to be searched for eigenvalues; emin ≤ emax.

NOTE:

Users are advised to avoid situations in which eigenvalues nearly coincide with the interval endpoints. This may lead to unpredictable selection or omission of such eigenvalues. Users should instead specify a slightly larger interval than needed and, if required, pick valid eigenvalues and their corresponding eigenvectors for subsequent use.

m0

INTEGER

On entry, specifies the initial guess for subspace size to be used, 0 < m0≤n. Set m0 ≥ m where m is the total number of eigenvalues located in the interval [emin, emax]. If the initial guess is wrong, Extended Eigensolver routines return info=3.

q

REAL for sfeast_srci

DOUBLE PRECISION for dfeast_srci

COMPLEX for cfeast_hrci

COMPLEX*16 for zfeast_hrci

On entry, if fpm(5)=1, the array q of size n by m contains a basis of guess subspace where n is the order of the input matrix.

Output Parameters

ijob

On exit, the parameter carries the status flag that indicates the condition of the return. The status information is divided into three categories:

A zero value indicates successful completion of the task.
A positive value indicates that the solver requires a matrix-vector multiplication or solving a specific system with a complex coefficient.
A negative value indicates successful initiation.

A non-zero value of ijob specifically means the following:

ijob = 10 - factorize the complex matrix Z_e*B - A at a given contour point Z_e and return the control to the ?feast_srci/?feast_hrci routine where Z_e is a complex number meaning contour point and its value is defined internally in ?feast_srci/?feast_hrci.
ijob =11 - solve the complex linear system (Z_e*B - A)*y = workc(n, m0), put the solution in workc(n, m0) and return the control to the ?feast_srci/?feast_hrci routine.
ijob =20 - factorize the complex matrix (Z_e*B - A)^H at a given contour point Z_e and return the control to the ?feast_srci/?feast_hrci routine where Z_e is a complex number meaning contour point and its value is defined internally in ?feast_srci/?feast_hrci.

The symbol X^H means transpose conjugate of matrix X.
ijob = 21 - solve the complex linear system(Z_e*B - A)^H*y = workc(n, m0), put the solution in workc(n, m0) and return the control to the ?feast_srci/?feast_hrci routine. The case ijob=20 becomes obsolete if the solve can be performed using the factorization computed for ijob=10.

The symbol X^H mean transpose conjugate of matrix X.
ijob = 30 - multiply matrix A by q(n, i:j), put the result in work(n, i:j), and return the control to the ?feast_srci/?feast_hrci routine.

i is fpm(25), and j is fpm(24) + fpm(25) - 1.
ijob = 40 - multiply matrix B by q(n, i:j), put the result in work(n, i:j) and return the control to the ?feast_srci/?feast_hrci routine. If a standard eigenvalue problem is solved, just return work = q.

i is fpm(25), and j is fpm(24) + fpm(25) - 1.
ijob = -2 - rerun the ?feast_srci/?feast_hrci task with the same parameters.

ze

COMPLEX for sfeast_srci and cfeast_hrci

COMPLEX*16 for dfeast_srci and zfeast_hrci

Defines the coordinate along the complex contour. All values of ze are generated by ?feast_srci/?feast_hrci internally.

fpm

On output, contains coordinates of columns of work array needed for iterative refinement. (See Extended Eigensolver RCI Interface Description.)

epsout

REAL for sfeast_srci and cfeast_hrci

DOUBLE PRECISION for dfeast_srci and zfeast_hrci

On output, contains the relative error on the trace: |trace_i - trace_i-1| /max(|emin|, |emax|)

loop

INTEGER

On output, contains the number of refinement loop executed. Ignored on input.

lambda

REAL for sfeast_srci and cfeast_hrci

DOUBLE PRECISION for dfeast_srci and zfeast_hrci

Array of length m0. On output, the first m entries of lambda are eigenvalues found in the interval.

q

On output, q contains all eigenvectors corresponding to lambda.

m

INTEGER

The total number of eigenvalues found in the interval [emin, emax]: 0 ≤ m ≤ m0.

res

REAL for sfeast_srci and cfeast_hrci

DOUBLE PRECISION for dfeast_srci and zfeast_hrci

Array of length m0. On exit, the first m components contain the relative residual vector:

generalized eigenvalue problem:
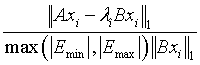
standard eigenvalue problem:

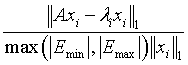
for i=1, 2, …, m, and where m is the total number of eigenvalues found in the search interval.

info

INTEGER

If info=0, the execution is successful. If info ≠ 0, see Output Eigensolver info Details.

Parent topic: Extended Eigensolver RCI Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?feast_srci/?feast_hrci

Syntax

Include Files

Description

Input Parameters

Output Parameters