?latrd

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-2BD9E50B-725C-4239-B488-4DA15947AC79

View Details

?latrd

Reduces the first nb rows and columns of a symmetric/Hermitian matrix A to real tridiagonal form by an orthogonal/unitary similarity transformation.

Syntax

call slatrd( uplo, n, nb, a, lda, e, tau, w, ldw )

call dlatrd( uplo, n, nb, a, lda, e, tau, w, ldw )

call clatrd( uplo, n, nb, a, lda, e, tau, w, ldw )

call zlatrd( uplo, n, nb, a, lda, e, tau, w, ldw )

Include Files

mkl.fi

Description

The routine ?latrd reduces nb rows and columns of a real symmetric or complex Hermitian matrix A to symmetric/Hermitian tridiagonal form by an orthogonal/unitary similarity transformation Q^T*A*Q for real flavors, Q^H*A*Q for complex flavors, and returns the matrices V and W which are needed to apply the transformation to the unreduced part of A.

If uplo = 'U', ?latrd reduces the last nb rows and columns of a matrix, of which the upper triangle is supplied;

if uplo = 'L', ?latrd reduces the first nb rows and columns of a matrix, of which the lower triangle is supplied.

This is an auxiliary routine called by ?sytrd/?hetrd.

Input Parameters

uplo

CHARACTER*1.

Specifies whether the upper or lower triangular part of the symmetric/Hermitian matrix A is stored:

= 'U': upper triangular

= 'L': lower triangular

n

INTEGER. The order of the matrix A.

nb

INTEGER. The number of rows and columns to be reduced.

a

REAL for slatrd

DOUBLE PRECISION for dlatrd

COMPLEX for clatrd

DOUBLE COMPLEX for zlatrd.

Array, DIMENSION (lda, n).

On entry, the symmetric/Hermitian matrix A

If uplo = 'U', the leading n-by-n upper triangular part of a contains the upper triangular part of the matrix A, and the strictly lower triangular part of a is not referenced.

If uplo = 'L', the leading n-by-n lower triangular part of a contains the lower triangular part of the matrix A, and the strictly upper triangular part of a is not referenced.

lda

INTEGER. The leading dimension of the array a. lda≥ (1,n).

ldw

INTEGER.

The leading dimension of the output array w. ldw≥ max(1,n).

Output Parameters

a

On exit, if uplo = 'U', the last nb columns have been reduced to tridiagonal form, with the diagonal elements overwriting the diagonal elements of a; the elements above the diagonal with the array tau, represent the orthogonal/unitary matrix Q as a product of elementary reflectors;

if uplo = 'L', the first nb columns have been reduced to tridiagonal form, with the diagonal elements overwriting the diagonal elements of a; the elements below the diagonal with the array tau, represent the orthogonal/unitary matrix Q as a product of elementary reflectors.

e

REAL for slatrd/clatrd

DOUBLE PRECISION for dlatrd/zlatrd.

If uplo = 'U', e(n-nb:n-1) contains the superdiagonal elements of the last nb columns of the reduced matrix;

if uplo = 'L', e(1:nb) contains the subdiagonal elements of the first nb columns of the reduced matrix.

tau

REAL for slatrd

DOUBLE PRECISION for dlatrd

COMPLEX for clatrd

DOUBLE COMPLEX for zlatrd.

Array, DIMENSION (lda, n).

The scalar factors of the elementary reflectors, stored in tau(n-nb:n-1) if uplo = 'U', and in tau(1:nb) if uplo = 'L'.

w

REAL for slatrd

DOUBLE PRECISION for dlatrd

COMPLEX for clatrd

DOUBLE COMPLEX for zlatrd.

Array, DIMENSION (ldw, n).

The n-by-nb matrix W required to update the unreduced part of A.

Application Notes

If uplo = 'U', the matrix Q is represented as a product of elementary reflectors

Q = H(n)*H(n-1)*...*H(n-nb+1)

Each H(i) has the form

H(i) = I - tau*v*v'

where tau is a real/complex scalar, and v is a real/complex vector with v(i:n) = 0 and v(i-1) = 1; v(1: i-1) is stored on exit in a(1: i-1, i), and tau in tau(i-1).

If uplo = 'L', the matrix Q is represented as a product of elementary reflectors

Q = H(1)*H(2)*...*H(nb)

Each H(i) has the form H(i) = I - tau*v*v'

where tau is a real/complex scalar, and v is a real/complex vector with v(1: i) = 0 and v(i+1) = 1; v( i+1:n) is stored on exit in a(i+1:n, i), and tau in tau(i).

The elements of the vectors v together form the n-by-nb matrix V which is needed, with W, to apply the transformation to the unreduced part of the matrix, using a symmetric/Hermitian rank-2k update of the form:

A := A - VW' - WV'.

The contents of a on exit are illustrated by the following examples with n = 5 and nb = 2:

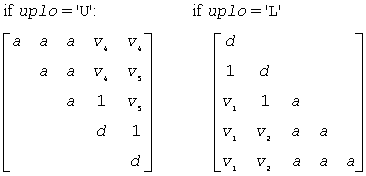
where d denotes a diagonal element of the reduced matrix, a denotes an element of the original matrix that is unchanged, and v_i denotes an element of the vector defining H(i).

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?latrd

Syntax

Include Files

Description

Input Parameters

Output Parameters

Application Notes