?gebrd

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-03C78F41-D16C-4BFE-B087-BE4F5A6A0B9B

View Details

?gebrd

Reduces a general matrix to bidiagonal form.

Syntax

call sgebrd(m, n, a, lda, d, e, tauq, taup, work, lwork, info)

call dgebrd(m, n, a, lda, d, e, tauq, taup, work, lwork, info)

call cgebrd(m, n, a, lda, d, e, tauq, taup, work, lwork, info)

call zgebrd(m, n, a, lda, d, e, tauq, taup, work, lwork, info)

call gebrd(a [, d] [,e] [,tauq] [,taup] [,info])

Include Files

mkl.fi, lapack.f90

Description

The routine reduces a general m-by-n matrix A to a bidiagonal matrix B by an orthogonal (unitary) transformation.

If m≥n, the reduction is given by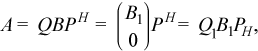

where B₁ is an n-by-n upper diagonal matrix, Q and P are orthogonal or, for a complex A, unitary matrices; Q₁ consists of the first n columns of Q.

If m < n, the reduction is given by

A = Q*B*P^H = Q*(B₁0)*P^H = Q₁*B₁*P₁^H,

where B₁ is an m-by-m lower diagonal matrix, Q and P are orthogonal or, for a complex A, unitary matrices; P₁ consists of the first m columns of P.

The routine does not form the matrices Q and P explicitly, but represents them as products of elementary reflectors. Routines are provided to work with the matrices Q and P in this representation:

If the matrix A is real,

to compute Q and P explicitly, call orgbr.
to multiply a general matrix by Q or P, call ormbr.

If the matrix A is complex,

to compute Q and P explicitly, call ungbr.
to multiply a general matrix by Q or P, call unmbr.

Input Parameters

m

INTEGER. The number of rows in the matrix A (m≥ 0).

n

INTEGER. The number of columns in A (n≥ 0).

a, work

REAL for sgebrd

DOUBLE PRECISION for dgebrd

COMPLEX for cgebrd

DOUBLE COMPLEX for zgebrd.

Arrays:

a(lda,*) contains the matrix A.

The second dimension of a must be at least max(1, n).

work is a workspace array, its dimension max(1, lwork).

lda

INTEGER. The leading dimension of a; at least max(1, m).

lwork

INTEGER.

The dimension of work; at least max(1, m, n).

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla.

See Application Notes for the suggested value of lwork.

Output Parameters

a

If m≥n, the diagonal and first super-diagonal of a are overwritten by the upper bidiagonal matrix B. The elements below the diagonal, with the array tauq, represent the orthogonal matrix Q as a product of elementary reflectors, and the elements above the first superdiagonal, with the array taup, represent the orthogonal matrix P as a product of elementary reflectors.

If m < n, the diagonal and first sub-diagonal of a are overwritten by the lower bidiagonal matrix B. The elements below the first subdiagonal, with the array tauq, represent the orthogonal matrix Q as a product of elementary reflectors, and the elements above the diagonal, with the array taup, represent the orthogonal matrix P as a product of elementary reflectors.

d

REAL for single-precision flavors

DOUBLE PRECISION for double-precision flavors.

Array, size at least max(1, min(m, n)).

Contains the diagonal elements of B.

e

REAL for single-precision flavors

DOUBLE PRECISION for double-precision flavors.

Array, size at least max(1, min(m, n) - 1). Contains the off-diagonal elements of B.

tauq, taup

REAL for sgebrd

DOUBLE PRECISION for dgebrd

COMPLEX for cgebrd

DOUBLE COMPLEX for zgebrd.

Arrays, size at least max (1, min(m, n)). The scalar factors of the elementary reflectors which represent the orthogonal or unitary matrices P and Q.

work(1)

If info = 0, on exit work(1) contains the minimum value of lwork required for optimum performance. Use this lwork for subsequent runs.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine gebrd interface are the following:

a: Holds the matrix A of size (m,n).
d: Holds the vector of length min(m,n).
e: Holds the vector of length min(m,n)-1.
tauq: Holds the vector of length min(m,n).
taup: Holds the vector of length min(m,n).

Application Notes

For better performance, try using lwork = (m + n)*blocksize, where blocksize is a machine-dependent value (typically, 16 to 64) required for optimum performance of the blocked algorithm.

If you are in doubt how much workspace to supply, use a generous value of lwork for the first run or set lwork = -1.

If you choose the first option and set any of admissible lwork sizes, which is no less than the minimal value described, the routine completes the task, though probably not so fast as with a recommended workspace, and provides the recommended workspace in the first element of the corresponding array work on exit. Use this value (work(1)) for subsequent runs.

If you set lwork = -1, the routine returns immediately and provides the recommended workspace in the first element of the corresponding array (work). This operation is called a workspace query.

Note that if you set lwork to less than the minimal required value and not -1, the routine returns immediately with an error exit and does not provide any information on the recommended workspace.

The computed matrices Q, B, and P satisfy QBP^H = A + E, where ||E||₂ = c(n)ε ||A||₂, c(n) is a modestly increasing function of n, and ε is the machine precision.

The approximate number of floating-point operations for real flavors is

(4/3)*n²*(3*m - n) for m≥n,

(4/3)*m²*(3*n - m) for m < n.

The number of operations for complex flavors is four times greater.

If n is much less than m, it can be more efficient to first form the QR factorization of A by calling geqrf and then reduce the factor R to bidiagonal form. This requires approximately 2*n²*(m + n) floating-point operations.

If m is much less than n, it can be more efficient to first form the LQ factorization of A by calling gelqf and then reduce the factor L to bidiagonal form. This requires approximately 2*m²*(m + n) floating-point operations.

Parent topic: Singular Value Decomposition: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?gebrd

Syntax

Include Files

Description

Input Parameters

Output Parameters

LAPACK 95 Interface Notes

Application Notes