?orghr

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-9695C009-3EE0-4A95-ABB8-A1E1C7561A87

View Details

?orghr

Generates the real orthogonal matrix Q determined by ?gehrd.

Syntax

call sorghr(n, ilo, ihi, a, lda, tau, work, lwork, info)

call dorghr(n, ilo, ihi, a, lda, tau, work, lwork, info)

call orghr(a, tau [,ilo] [,ihi] [,info])

Include Files

mkl.fi, lapack.f90

Description

The routine explicitly generates the orthogonal matrix Q that has been determined by a preceding call to sgehrd/dgehrd. (The routine ?gehrd reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation, A = Q*H*Q^T, and represents the matrix Q as a product of ihi-iloelementary reflectors. Here ilo and ihi are values determined by sgebal/dgebal when balancing the matrix; if the matrix has not been balanced, ilo = 1 and ihi = n.)

The matrix Q generated by ?orghr has the structure:

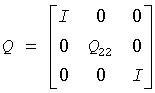
where Q₂₂ occupies rows and columns ilo to ihi.

Input Parameters

n

INTEGER. The order of the matrix Q (n≥ 0).

ilo, ihi

INTEGER. These must be the same parameters ilo and ihi, respectively, as supplied to ?gehrd. (If n > 0, then 1 ≤ilo≤ihi≤n; if n = 0, ilo = 1 and ihi = 0.)

a, tau, work

REAL for sorghr

DOUBLE PRECISION for dorghr

Arrays: a(lda,*) contains details of the vectors which define the elementary reflectors, as returned by ?gehrd.

The second dimension of a must be at least max(1, n).

tau(*) contains further details of the elementary reflectors, as returned by ?gehrd.

The dimension of tau must be at least max (1, n-1).

work is a workspace array, its dimension max(1, lwork).

lda

INTEGER. The leading dimension of a; at least max(1, n).

lwork

INTEGER. The size of the work array;

lwork≥ max(1, ihi-ilo).

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla.

See Application Notes for the suggested value of lwork.

Output Parameters

a

Overwritten by the n-by-n orthogonal matrix Q.

work(1)

If info = 0, on exit work(1) contains the minimum value of lwork required for optimum performance. Use this lwork for subsequent runs.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine orghr interface are the following:

a: Holds the matrix A of size (n,n).
tau: Holds the vector of length (n-1).
ilo: Default value for this argument is ilo = 1.
ihi: Default value for this argument is ihi = n.

Application Notes

For better performance, try using lwork =(ihi-ilo)*blocksize where blocksize is a machine-dependent value (typically, 16 to 64) required for optimum performance of the blocked algorithm.

If you are in doubt how much workspace to supply, use a generous value of lwork for the first run or set lwork = -1.

If you choose the first option and set any of admissible lwork sizes, which is no less than the minimal value described, the routine completes the task, though probably not so fast as with a recommended workspace, and provides the recommended workspace in the first element of the corresponding array work on exit. Use this value (work(1)) for subsequent runs.

If you set lwork = -1, the routine returns immediately and provides the recommended workspace in the first element of the corresponding array (work). This operation is called a workspace query.

Note that if you set lwork to less than the minimal required value and not -1, the routine returns immediately with an error exit and does not provide any information on the recommended workspace.

The computed matrix Q differs from the exact result by a matrix E such that ||E||₂ = O(ε), where ε is the machine precision.

The approximate number of floating-point operations is (4/3)(ihi-ilo)³.

The complex counterpart of this routine is unghr.

Parent topic: Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?orghr

Syntax

Include Files

Description

Input Parameters

Output Parameters

LAPACK 95 Interface Notes

Application Notes