?ggsvp3

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-EA9110B0-4EE8-46EE-851E-327F44597C7E

View Details

?ggsvp3

Performs preprocessing for a generalized SVD.

Syntax

call sggsvp3 (jobu, jobv, jobq, m, p, n, a, lda, b, ldb, tola, tolb, k, l, u, ldu, v, ldv, q, ldq, iwork, tau, work, lwork, info )

call dggsvp3 (jobu, jobv, jobq, m, p, n, a, lda, b, ldb, tola, tolb, k, l, u, ldu, v, ldv, q, ldq, iwork, tau, work, lwork, info )

call cggsvp3 (jobu, jobv, jobq, m, p, n, a, lda, b, ldb, tola, tolb, k, l, u, ldu, v, ldv, q, ldq, iwork, rwork, tau, work, lwork, info )

call zggsvp3 (jobu, jobv, jobq, m, p, n, a, lda, b, ldb, tola, tolb, k, l, u, ldu, v, ldv, q, ldq, iwork, rwork, tau, work, lwork, info )

Include Files

mkl_lapack.fi

Include Files

mkl.fi

Description

?ggsvp3 computes orthogonal or unitary matrices U, V, and Q such that

for real flavors:

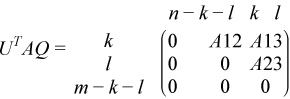if m - k - l≥ 0;

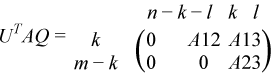if m - k - l< 0;

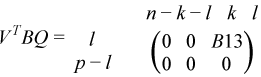
for complex flavors:

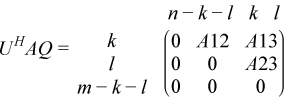if m - k - l≥ 0;

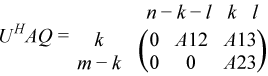if m - k-l< 0;

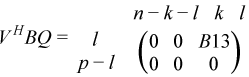
where the k-by-k matrix A12 and l-by-l matrix B13 are nonsingular upper triangular; A23 is l-by-l upper triangular if m-k-l≥ 0, otherwise A23 is (m-k-by-l upper trapezoidal. k + l = the effective numerical rank of the (m + p)-by-n matrix (A^T,B^T)^T for real flavors or (A^H,B^H)^H for complex flavors.

This decomposition is the preprocessing step for computing the Generalized Singular Value Decomposition (GSVD), see ?ggsvd3.

Input Parameters

jobu

CHARACTER*1. = 'U': Orthogonal/unitary matrix U is computed;

= 'N': U is not computed.

jobv

CHARACTER*1. = 'V': Orthogonal/unitary matrix V is computed;

= 'N': V is not computed.

jobq

CHARACTER*1. = 'Q': Orthogonal/unitary matrix Q is computed;

= 'N': Q is not computed.

m

INTEGER. The number of rows of the matrix A.

m≥ 0.

p

INTEGER. The number of rows of the matrix B.

p≥ 0.

n

INTEGER. The number of columns of the matrices A and B.

n≥ 0.

a

REAL for sggsvp3

DOUBLE PRECISION for dggsvp3

COMPLEX for cggsvp3

DOUBLE COMPLEX for zggsvp3

Array, size (lda, n).

On entry, the m-by-n matrix A.

lda

INTEGER. The leading dimension of the array a.

lda≥ max(1,m).

b

REAL for sggsvp3

DOUBLE PRECISION for dggsvp3

COMPLEX for cggsvp3

DOUBLE COMPLEX for zggsvp3

Array, size (ldb, n).

On entry, the p-by-n matrix B.

ldb

INTEGER. The leading dimension of the array b.

ldb≥ max(1,p).

tola, tolb

REAL for sggsvp3

DOUBLE PRECISION for dggsvp3

REAL for cggsvp3

DOUBLE PRECISION for zggsvp3

tola and tolb are the thresholds to determine the effective numerical rank of matrix B and a subblock of A. Generally, they are set to

tola = max(m,n)*norm(a)*MACHEPS,

tolb = max(p,n)*norm(b)*MACHEPS.

The size of tola and tolb may affect the size of backward errors of the decomposition.

ldu

INTEGER. The leading dimension of the array u.

ldu≥ max(1,m) if jobu = 'U'; ldu≥ 1 otherwise.

ldv

INTEGER. The leading dimension of the array v.

ldv≥ max(1,p) if jobv = 'V'; ldv≥ 1 otherwise.

ldq

INTEGER. The leading dimension of the array q.

ldq≥ max(1,n) if jobq = 'Q'; ldq≥ 1 otherwise.

iwork

INTEGER. Array, size (n).

rwork

for sggsvp3

for dggsvp3

REAL for cggsvp3

DOUBLE PRECISION for zggsvp3

Array, size (2*n).

tau

REAL for sggsvp3

DOUBLE PRECISION for dggsvp3

COMPLEX for cggsvp3

DOUBLE COMPLEX for zggsvp3

Array, size (n).

The scalar factors of the elementary reflectors.

work

REAL for sggsvp3

DOUBLE PRECISION for dggsvp3

COMPLEX for cggsvp3

DOUBLE COMPLEX for zggsvp3

Array, size (MAX(1,lwork)).

lwork

INTEGER. The dimension of the array work.

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla.

Output Parameters

a	On exit, a contains the triangular (or trapezoidal) matrix described in the Description section.
b	On exit, b contains the triangular matrix described in the Description section.
k, l	INTEGER. On exit, k and l specify the dimension of the subblocks described in Description section. k + l = effective numerical rank of (`A`^T,`B`^T)^T for real flavors or (`A`^H,`B`^H)^H for complex flavors.
u	REAL for sggsvp3 DOUBLE PRECISION for dggsvp3 COMPLEX for cggsvp3 DOUBLE COMPLEX for zggsvp3 Array, size (ldu, m). If jobu = 'U', u contains the orthogonal/unitary matrix `U`. If jobu = 'N', u is not referenced.
v	REAL for sggsvp3 DOUBLE PRECISION for dggsvp3 COMPLEX for cggsvp3 DOUBLE COMPLEX for zggsvp3 Array, size (ldv, p). If jobv = 'V', v contains the orthogonal/unitary matrix `V`. If jobv = 'N', v is not referenced.
q	REAL for sggsvp3 DOUBLE PRECISION for dggsvp3 COMPLEX for cggsvp3 DOUBLE COMPLEX for zggsvp3 Array, size (ldq, n). If jobq = 'Q', q contains the orthogonal/unitary matrix `Q`. If jobq = 'N', q is not referenced.
work	On exit, if info = 0, work(1) returns the optimal lwork.
info	INTEGER. = 0: successful exit. < 0: if info = -`i`, the `i`-th argument had an illegal value.

Application Notes

The subroutine uses LAPACK subroutine ?geqp3 for the QR factorization with column pivoting to detect the effective numerical rank of the A matrix. It may be replaced by a better rank determination strategy.

?ggsvp3 replaces the deprecated subroutine ?ggsvp.

Parent topic: Generalized Singular Value Decomposition: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?ggsvp3

Syntax

Include Files

Include Files

Description

Input Parameters

Output Parameters

Application Notes