?trsna

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-859D90A3-6336-4C9A-95D2-ABF40FE19965

View Details

?trsna

Estimates condition numbers for specified eigenvalues and right eigenvectors of an upper (quasi-) triangular matrix.

Syntax

lapack_int LAPACKE_strsna( int matrix_layout, char job, char howmny, const lapack_logical* select, lapack_int n, const float* t, lapack_int ldt, const float* vl, lapack_int ldvl, const float* vr, lapack_int ldvr, float* s, float* sep, lapack_int mm, lapack_int* m );

lapack_int LAPACKE_dtrsna( int matrix_layout, char job, char howmny, const lapack_logical* select, lapack_int n, const double* t, lapack_int ldt, const double* vl, lapack_int ldvl, const double* vr, lapack_int ldvr, double* s, double* sep, lapack_int mm, lapack_int* m );

lapack_int LAPACKE_ctrsna( int matrix_layout, char job, char howmny, const lapack_logical* select, lapack_int n, const lapack_complex_float* t, lapack_int ldt, const lapack_complex_float* vl, lapack_int ldvl, const lapack_complex_float* vr, lapack_int ldvr, float* s, float* sep, lapack_int mm, lapack_int* m );

lapack_int LAPACKE_ztrsna( int matrix_layout, char job, char howmny, const lapack_logical* select, lapack_int n, const lapack_complex_double* t, lapack_int ldt, const lapack_complex_double* vl, lapack_int ldvl, const lapack_complex_double* vr, lapack_int ldvr, double* s, double* sep, lapack_int mm, lapack_int* m );

Include Files

mkl.h

Description

The routine estimates condition numbers for specified eigenvalues and/or right eigenvectors of an upper triangular matrix T (or, for real flavors, upper quasi-triangular matrix T in canonical Schur form). These are the same as the condition numbers of the eigenvalues and right eigenvectors of an original matrix A = Z*T*Z^H (with unitary or, for real flavors, orthogonal Z), from which T may have been derived.

The routine computes the reciprocal of the condition number of an eigenvalue λ_i as s_i = |v^T*u|/(||u||_E||v||_E) for real flavors and s_i = |v^H*u|/(||u||_E||v||_E) for complex flavors,

where:

u and v are the right and left eigenvectors of T, respectively, corresponding to λ_i.
v^T/v^H denote transpose/conjugate transpose of v, respectively.

This reciprocal condition number always lies between zero (ill-conditioned) and one (well-conditioned).

An approximate error estimate for a computed eigenvalue λ_i is then given by ε*||T||/s_i, where ε is the machine precision.

To estimate the reciprocal of the condition number of the right eigenvector corresponding to λ_i, the routine first calls trexc to reorder the diagonal elements of matrix T so that λ_i is in the leading position:

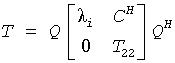
The reciprocal condition number of the eigenvector is then estimated as sep_i, the smallest singular value of the matrix T₂₂ - λ_i*I.

An approximate error estimate for a computed right eigenvector u corresponding to λ_i is then given by ε*||T||/sep_i.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

job

Must be 'E' or 'V' or 'B'.

If job = 'E', then condition numbers for eigenvalues only are computed.

If job = 'V', then condition numbers for eigenvectors only are computed.

If job = 'B', then condition numbers for both eigenvalues and eigenvectors are computed.

howmny

Must be 'A' or 'S'.

If howmny = 'A', then the condition numbers for all eigenpairs are computed.

If howmny = 'S', then condition numbers for selected eigenpairs (as specified by select) are computed.

select

Array, size at least max (1, n) if howmny = 'S' and at least 1 otherwise.

Specifies the eigenpairs for which condition numbers are to be computed if howmny= 'S'.

For real flavors:

To select condition numbers for the eigenpair corresponding to the real eigenvalue λ_j, select[j] must be set 1;

to select condition numbers for the eigenpair corresponding to a complex conjugate pair of eigenvalues λ_j and λ_{j + 1}), select[j - 1] and/or select[j] must be set 1

For complex flavors

To select condition numbers for the eigenpair corresponding to the eigenvalue λ_j, select[j] must be set 1select is not referenced if howmny = 'A'.

n

The order of the matrix T (n≥ 0).

t, vl, vr

Arrays:

t (size max(1, ldt*n)) contains the n-by-n matrix T.

vl(size max(1, ldvl*mm) for column major layout and max(1, ldvl*n) for row major layout)

If job = 'E' or 'B', then vl must contain the left eigenvectors of T (or of any matrix Q*T*Q^H with Q unitary or orthogonal) corresponding to the eigenpairs specified by howmny and select. The eigenvectors must be stored in consecutive columns of vl, as returned by trevc or hsein.

The array vl is not referenced if job = 'V'.

vr(size max(1, ldvr*mm) for column major layout and max(1, ldvr*n) for row major layout)

If job = 'E' or 'B', then vr must contain the right eigenvectors of T (or of any matrix Q*T*Q^H with Q unitary or orthogonal) corresponding to the eigenpairs specified by howmny and select. The eigenvectors must be stored in consecutive columns of vr, as returned by trevc or hsein.

The array vr is not referenced if job = 'V'.

ldt

The leading dimension of t; at least max(1, n).

ldvl

The leading dimension of vl.

If job = 'E' or 'B', ldvl≥ max(1,n) for column major layout and ldvl≥ max(1, mm) for row major layout .

If job = 'V', ldvl≥ 1.

ldvr

The leading dimension of vr.

If job = 'E' or 'B', ldvr≥ max(1,n) for column major layout and ldvr≥ max(1, mm) for row major layout .

If job = 'R', ldvr≥ 1.

mm

The number of elements in the arrays s and sep, and the number of columns in vl and vr (if used). Must be at least m (the precise number required).

If howmny = 'A', mm = n;

if howmny = 'S', for real flavorsmm is obtained by counting 1 for each selected real eigenvalue and 2 for each selected complex conjugate pair of eigenvalues.

for complex flavorsmm is the number of selected eigenpairs (see select). Constraint:

0 ≤mm≤n.

Output Parameters

s

Array, size at least max(1, mm) if job = 'E' or 'B' and at least 1 if job = 'V'.

Contains the reciprocal condition numbers of the selected eigenvalues if job = 'E' or 'B', stored in consecutive elements of the array. Thus s[j - 1], sep[j - 1] and the j-th columns of vl and vr all correspond to the same eigenpair (but not in general the j th eigenpair unless all eigenpairs have been selected).

For real flavors: for a complex conjugate pair of eigenvalues, two consecutive elements of s are set to the same value. The array s is not referenced if job = 'V'.

sep

Array, size at least max(1, mm) if job = 'V' or 'B' and at least 1 if job = 'E'. Contains the estimated reciprocal condition numbers of the selected right eigenvectors if job = 'V' or 'B', stored in consecutive elements of the array.

For real flavors: for a complex eigenvector, two consecutive elements of sep are set to the same value; if the eigenvalues cannot be reordered to compute sep[j - 1], then sep[j - 1] is set to zero; this can only occur when the true value would be very small anyway. The array sep is not referenced if job = 'E'.

m

For complex flavors: the number of selected eigenpairs.

If howmny = 'A', m is set to n.

For real flavors: the number of elements of s and/or sep actually used to store the estimated condition numbers.

If howmny = 'A', m is set to n.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Application Notes

The computed values sep_i may overestimate the true value, but seldom by a factor of more than 3.

Parent topic: Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?trsna

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes