?ggsvp

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-1132D836-224B-4E5A-9B53-6987AF272587

View Details

?ggsvp

Computes the preprocessing decomposition for the generalized SVD (deprecated).

Syntax

lapack_int LAPACKE_sggsvp( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int p, lapack_int n, float* a, lapack_int lda, float* b, lapack_int ldb, float tola, float tolb, lapack_int* k, lapack_int* l, float* u, lapack_int ldu, float* v, lapack_int ldv, float* q, lapack_int ldq );

lapack_int LAPACKE_dggsvp( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int p, lapack_int n, double* a, lapack_int lda, double* b, lapack_int ldb, double tola, double tolb, lapack_int* k, lapack_int* l, double* u, lapack_int ldu, double* v, lapack_int ldv, double* q, lapack_int ldq );

lapack_int LAPACKE_cggsvp( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int p, lapack_int n, lapack_complex_float* a, lapack_int lda, lapack_complex_float* b, lapack_int ldb, float tola, float tolb, lapack_int* k, lapack_int* l, lapack_complex_float* u, lapack_int ldu, lapack_complex_float* v, lapack_int ldv, lapack_complex_float* q, lapack_int ldq );

lapack_int LAPACKE_zggsvp( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int p, lapack_int n, lapack_complex_double* a, lapack_int lda, lapack_complex_double* b, lapack_int ldb, double tola, double tolb, lapack_int* k, lapack_int* l, lapack_complex_double* u, lapack_int ldu, lapack_complex_double* v, lapack_int ldv, lapack_complex_double* q, lapack_int ldq );

Include Files

mkl.h

Description

This routine is deprecated; use ggsvp3.

The routine computes orthogonal matrices U, V and Q such that

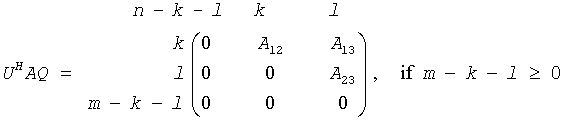
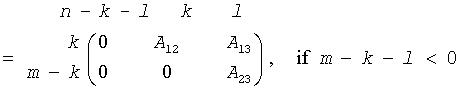
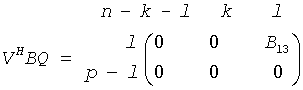
where the k-by-k matrix A₁₂ and l-by-l matrix B₁₃ are nonsingular upper triangular; A₂₃ is l-by-l upper triangular if m-k-l≥0, otherwise A₂₃ is (m-k)-by-l upper trapezoidal. The sum k+l is equal to the effective numerical rank of the (m+p)-by-n matrix (A^H,B^H)^H.

This decomposition is the preprocessing step for computing the Generalized Singular Value Decomposition (GSVD), see subroutine ?tgsja.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

jobu

Must be 'U' or 'N'.

If jobu = 'U', orthogonal/unitary matrix U is computed.

If jobu = 'N', U is not computed.

jobv

Must be 'V' or 'N'.

If jobv = 'V', orthogonal/unitary matrix V is computed.

If jobv = 'N', V is not computed.

jobq

Must be 'Q' or 'N'.

If jobq = 'Q', orthogonal/unitary matrix Q is computed.

If jobq = 'N', Q is not computed.

m

The number of rows of the matrix A (m≥ 0).

p

The number of rows of the matrix B (p≥ 0).

n

The number of columns of the matrices A and B (n≥ 0).

a, b

Arrays:

a(size at least max(1, lda*n) for column major layout and max(1, lda*m) for row major layout) contains the m-by-n matrix A.

b(size at least max(1, ldb*n) for column major layout and max(1, ldb*p) for row major layout) contains the p-by-n matrix B.

lda

The leading dimension of a; at least max(1, m)for column major layout and max(1, n) for row major layout.

ldb

The leading dimension of b; at least max(1, p)for column major layout and max(1, n) for row major layout.

tola, tolb

tola and tolb are the thresholds to determine the effective numerical rank of matrix B and a subblock of A. Generally, they are set to

tola = max(m, n)*||A||*MACHEPS,

tolb = max(p, n)*||B||*MACHEPS.

The size of tola and tolb may affect the size of backward errors of the decomposition.

ldu

The leading dimension of the output array u . ldu≥ max(1, m) if jobu = 'U'; ldu≥ 1 otherwise.

ldv

The leading dimension of the output array v . ldv≥ max(1, p) if jobv = 'V'; ldv≥ 1 otherwise.

ldq

The leading dimension of the output array q . ldq≥ max(1, n) if jobq = 'Q'; ldq≥ 1 otherwise.

Output Parameters

a

Overwritten by the triangular (or trapezoidal) matrix described in the Description section.

b

Overwritten by the triangular matrix described in the Description section.

k, l

On exit, k and l specify the dimension of subblocks. The sum k + l is equal to effective numerical rank of (A^H, B^H)^H.

u, v, q

Arrays:

If jobu = 'U', u (size max(1, ldu*m)) contains the orthogonal/unitary matrix U.

If jobu = 'N', u is not referenced.

If jobv = 'V', v (size max(1, ldv*p)) contains the orthogonal/unitary matrix V.

If jobv = 'N', v is not referenced.

If jobq = 'Q', q (size max(1, ldq*n)) contains the orthogonal/unitary matrix Q.

If jobq = 'N', q is not referenced.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Parent topic: Generalized Singular Value Decomposition: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?ggsvp

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values