p?larfg

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-B181C3B1-02F5-4A1F-A20F-8A5502827F94

View Details

p?larfg

Generates an elementary reflector (Householder matrix).

Syntax

void pslarfg (MKL_INT *n , float *alpha , MKL_INT *iax , MKL_INT *jax , float *x , MKL_INT *ix , MKL_INT *jx , MKL_INT *descx , MKL_INT *incx , float *tau );

void pdlarfg (MKL_INT *n , double *alpha , MKL_INT *iax , MKL_INT *jax , double *x , MKL_INT *ix , MKL_INT *jx , MKL_INT *descx , MKL_INT *incx , double *tau );

void pclarfg (MKL_INT *n , MKL_Complex8 *alpha , MKL_INT *iax , MKL_INT *jax , MKL_Complex8 *x , MKL_INT *ix , MKL_INT *jx , MKL_INT *descx , MKL_INT *incx , MKL_Complex8 *tau );

void pzlarfg (MKL_INT *n , MKL_Complex16 *alpha , MKL_INT *iax , MKL_INT *jax , MKL_Complex16 *x , MKL_INT *ix , MKL_INT *jx , MKL_INT *descx , MKL_INT *incx , MKL_Complex16 *tau );

Include Files

mkl_scalapack.h

Description

The p?larfgfunction generates a real/complex elementary reflector H of order n, such that

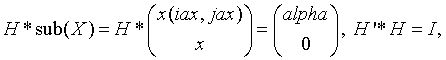
where alpha is a scalar (a real scalar - for complex flavors), and sub(X) is an (n-1)-element real/complex distributed vector X(ix:ix+n-2, jx) if incx = 1 and X(ix, jx:jx+n-2) if incx = m_x. H is represented in the form

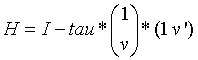
where tau is a real/complex scalar and v is a real/complex (n-1)-element vector. Note that H is not Hermitian.

If the elements of sub(X) are all zero (and X(iax, jax) is real for complex flavors), then tau = 0 and H is taken to be the unit matrix.

Otherwise 1 ≤ real(tau) ≤ 2 and abs(tau-1) ≤ 1.

Input Parameters

n

(global)

The global order of the elementary reflector. n ≥ 0.

iax, jax

(global)

The global row and column indices of X(iax, jax) in the global matrix X.

x

(local).

Pointer into the local memory to an array of size lld_x * LOCc(n_x). This array contains the local pieces of the distributed vector sub(X). Before entry, the incremented array sub(X) must contain vector x.

ix, jx

(global)

The row and column indices in the global matrix X indicating the first row and the first column of sub(X), respectively.

descx

(global and local)

Array of size dlen_. The array descriptor for the distributed matrix X.

incx

(global)

The global increment for the elements of x. Only two values of incx are supported in this version, namely 1 and m_x. incx must not be zero.

Output Parameters

alpha

(local)

On exit, alpha is computed in the process scope having the vector sub(X).

x

(local).

On exit, it is overwritten with the vector v.

tau

(local).

Array of size LOCc(jx) if incx = 1, and LOCr(ix) otherwise. This array contains the Householder scalars related to the Householder vectors.

tau is tied to the distributed matrix X.

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

p?larfg

Syntax

Include Files

Description

Input Parameters

Output Parameters

See Also