?orghr

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-9695C009-3EE0-4A95-ABB8-A1E1C7561A87

View Details

?orghr

Generates the real orthogonal matrix Q determined by ?gehrd.

Syntax

lapack_int LAPACKE_sorghr (int matrix_layout, lapack_int n, lapack_int ilo, lapack_int ihi, float* a, lapack_int lda, const float* tau);

lapack_int LAPACKE_dorghr (int matrix_layout, lapack_int n, lapack_int ilo, lapack_int ihi, double* a, lapack_int lda, const double* tau);

Include Files

mkl.h

Description

The routine explicitly generates the orthogonal matrix Q that has been determined by a preceding call to sgehrd/dgehrd. (The routine ?gehrd reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation, A = Q*H*Q^T, and represents the matrix Q as a product of ihi-iloelementary reflectors. Here ilo and ihi are values determined by sgebal/dgebal when balancing the matrix; if the matrix has not been balanced, ilo = 1 and ihi = n.)

The matrix Q generated by ?orghr has the structure:

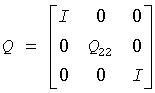
where Q₂₂ occupies rows and columns ilo to ihi.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

n

The order of the matrix Q (n≥ 0).

ilo, ihi

These must be the same parameters ilo and ihi, respectively, as supplied to ?gehrd. (If n > 0, then 1 ≤ilo≤ihi≤n; if n = 0, ilo = 1 and ihi = 0.)

a, tau

Arrays: a (size max(1, lda*n)) contains details of the vectors which define the elementary reflectors, as returned by ?gehrd.

tau contains further details of the elementary reflectors, as returned by ?gehrd.

The dimension of tau must be at least max (1, n-1).

lda

The leading dimension of a; at least max(1, n).

Output Parameters

a: Overwritten by the n-by-n orthogonal matrix Q.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Application Notes

The computed matrix Q differs from the exact result by a matrix E such that ||E||₂ = O(ε), where ε is the machine precision.

The approximate number of floating-point operations is (4/3)(ihi-ilo)³.

The complex counterpart of this routine is unghr.

Parent topic: Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?orghr

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes