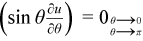Poisson Solver Implementation

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-3E012BD6-539C-4A78-AD42-8E19EDDE3A62

View Details

Poisson Solver Implementation

Poisson Solver routines enable approximate solving of certain two-dimensional and three-dimensional problems. Figure "Structure of the Poisson Solver" shows the general structure of the Poisson Solver.

Structure of the Poisson Solver

NOTE:

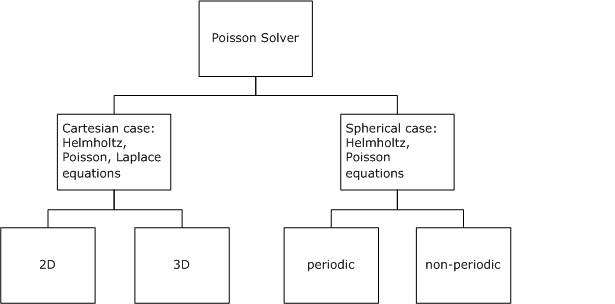
Although in the Cartesian case, both periodic and non-periodic solvers are also supported, they use the same interfaces.

Sections below provide details of the problems that can be solved using Intel® oneAPI Math Kernel Library (oneMKL) Poisson Solver.

Two-Dimensional Problems

Notational Conventions

The Poisson Solver interface description uses the following notation for boundaries of a rectangular domain a_x < x < b_x, a_y < y < b_y on a Cartesian plane:

bd_a_x = {x = a_x, a_y ≤ y ≤ b_y}, bd_b_x = {x = b_x, a_y ≤ y ≤ b_y}

bd_a_y = {a_x ≤ x ≤ b_x, y = a_y}, bd_b_y = {a_x ≤ x ≤ b_x, y = b_y}.

The following figure shows these boundaries:

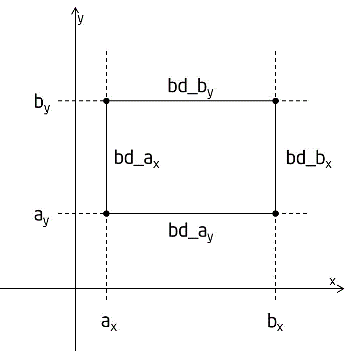
The wildcard "+" may stand for any of the symbols a_x, b_x, a_y, b_y, so bd_+ denotes any of the above boundaries.

The Poisson Solver interface description uses the following notation for boundaries of a rectangular domain a_φ < φ < b_φ, a_θ < θ < b_θ on a sphere 0 ≤ φ ≤ 2 π, 0 ≤ θ ≤ π:

bd_a_φ = {φ = a_φ, a_θ ≤ θ ≤ b_θ}, bd_b_φ = {φ = b_φ, a_θ ≤ θ ≤ b_θ},

bd_a_θ = {a_φ ≤ φ ≤ b_φ, θ = a_θ}, bd_b_θ = {a_φ ≤ φ ≤ b_φ, θ = b_θ}.

The wildcard "~" may stand for any of the symbols a_φ, b_φ, a_θ, b_θ, so bd_~ denotes any of the above boundaries.

Two-dimensional Helmholtz problem on a Cartesian plane

The two-dimensional (2D) Helmholtz problem is to find an approximate solution of the Helmholtz equation

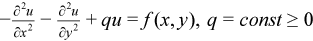
in a rectangle, that is, a rectangular domain a_x< x < b_x, a_y< y < b_y, with one of the following boundary conditions on each boundary bd_+:

The Dirichlet boundary condition
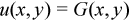
The Neumann boundary condition

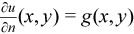
where

n= -x on bd_a_x, n= x on bd_b_x,

n= -y on bd_a_y, n= y on bd_b_y.
Periodic boundary conditions

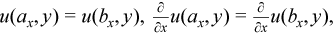
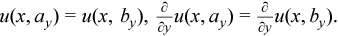
Two-dimensional Poisson problem on a Cartesian plane

The Poisson problem is a special case of the Helmholtz problem, when q=0. The 2D Poisson problem is to find an approximate solution of the Poisson equation

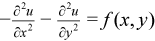
in a rectangle a_x< x < b_x, a_y< y < b_y with the Dirichlet, Neumann, or periodic boundary conditions on each boundary bd_+. In case of a problem with the Neumann boundary condition on the entire boundary, you can find the solution of the problem only up to a constant. In this case, the Poisson Solver will compute the solution that provides the minimal Euclidean norm of a residual.

Two-dimensional (2D) Laplace problem on a Cartesian plane

The Laplace problem is a special case of the Helmholtz problem, when q=0 and f(x, y)=0. The 2D Laplace problem is to find an approximate solution of the Laplace equation

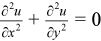
in a rectangle a_x< x < b_x, a_y< y < b_y with the Dirichlet, Neumann, or periodic boundary conditions on each boundary bd_+.

Helmholtz problem on a sphere

The Helmholtz problem on a sphere is to find an approximate solution of the Helmholtz equation

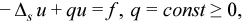
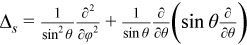
in a domain bounded by angles a_φ≤ φ ≤ b_φ, a_θ≤ θ ≤ b_θ (spherical rectangle), with boundary conditions for particular domains listed in Table "Details of Helmholtz Problem on a Sphere".

Details of Helmholtz Problem on a Sphere
Domain on a sphere	Boundary condition	Periodic/non-periodic case
Rectangular, that is, `b`_φ - `a`_φ < 2 `π` and `b`_θ - `a`_θ < `π`	Homogeneous Dirichlet boundary conditions on each boundary `bd_~`	non-periodic
Where `a`_φ = 0, `b`_φ = 2 `π`, and `b`_θ - `a`_θ < `π`	Homogeneous Dirichlet boundary conditions on the boundaries `bd_a`_θ and `bd_b`_θ	periodic
Entire sphere, that is, `a`_φ = 0, `b`_φ = 2 `π`, `a`_θ = 0, and `b`_θ = `π`	Boundary condition at the poles	periodic

Poisson problem on a sphere

The Poisson problem is a special case of the Helmholtz problem, when q=0. The Poisson problem on a sphere is to find an approximate solution of the Poisson equation

in a spherical rectangle a_φ≤ φ ≤ b_φ, a_θ≤ θ ≤ b_θ in cases listed in Table "Details of Helmholtz Problem on a Sphere". The solution to the Poisson problem on the entire sphere can be found up to a constant only. In this case, Poisson Solver will compute the solution that provides the minimal Euclidean norm of a residual.

Approximation of 2D problems

To find an approximate solution for any of the 2D problems, in the rectangular domain a uniform mesh can be defined for the Cartesian case as:

and for the spherical case as:

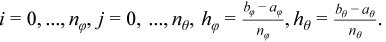
The Poisson Solver uses the standard five-point finite difference approximation on this mesh to compute the approximation to the solution:

In the Cartesian case, the values of the approximate solution will be computed in the mesh points (x_i , y_j) provided that you can supply the values of the right-hand side f(x, y) in these points and the values of the appropriate boundary functions G(x, y) and/or g(x,y) in the mesh points laying on the boundary of the rectangular domain.
In the spherical case, the values of the approximate solution will be computed in the mesh points (φ_i , θ_j) provided that you can supply the values of the right-hand side f(φ, θ) in these points.

NOTE:

The number of mesh intervals n_φ in the φ direction of a spherical mesh must be even in the periodic case. The Poisson Solver does not support spherical meshes that do not meet this condition.

Three-Dimensional Problems

Notational Conventions

The Poisson Solver interface description uses the following notation for boundaries of a parallelepiped domain a_x < x < b_x, a_y < y <b_y, a_z < z <b_z:

bd_a_x = {x = a_x, a_y ≤ y ≤ b_y, a_z ≤ z ≤ b_z}, bd_b_x = {x = b_x, a_y ≤ y ≤ b_y, a_z ≤ z ≤ b_z},

bd_a_y = {a_x ≤ x ≤ b_x, y = a_y, a_z ≤ z ≤ b_z}, bd_b_y = {a_x ≤ x ≤ b_x, y = b_y, a_z ≤ z ≤ b_z},

bd_a_z = {a_x ≤ x ≤ b_x, a_y ≤ y ≤ b_y, z = a_z}, bd_b_x = {a_x ≤ x ≤ b_x, a_y ≤ y ≤ b_y, z = b_z}.

The following figure shows these boundaries:

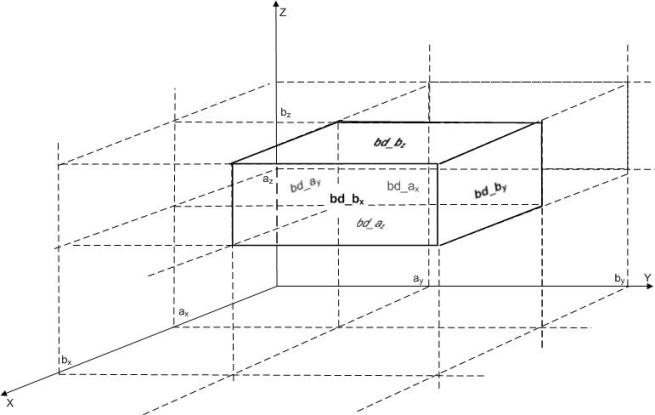
The wildcard "+" may stand for any of the symbols a_x, b_x, a_y, b_y, a_z, b_z, so bd_+ denotes any of the above boundaries.

Three-dimensional (3D) Helmholtz problem

The 3D Helmholtz problem is to find an approximate solution of the Helmholtz equation

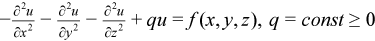
in a parallelepiped, that is, a parallelepiped domain a_x< x < b_x, a_y< y < b_y, a_z< z < b_z, with one of the following boundary conditions on each boundary bd_+:

The Dirichlet boundary condition
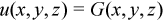
The Neumann boundary condition

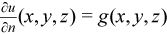
where

n= -x on bd_a_x, n= x on bd_b_x,

n= -y on bd_a_y, n= y on bd_b_y,

n= -z on bd_a_z, n= z on bd_b_z.
Periodic boundary conditions

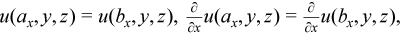
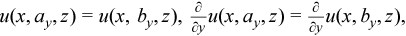
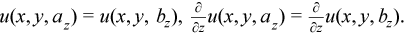
Three-dimensional (3D) Poisson problem

The Poisson problem is a special case of the Helmholtz problem, when q=0. The 3D Poisson problem is to find an approximate solution of the Poisson equation

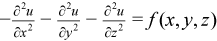
in a parallelepiped a_x< x < b_x , a_y< y < b_y, a_z< z < b_z with the Dirichlet, Neumann, or periodic boundary conditions on each boundary bd_+.

Three-dimensional (3D) Laplace problem

The Laplace problem is a special case of the Helmholtz problem, when q=0 and f(x, y, z)=0. The 3D Laplace problem is to find an approximate solution of the Laplace equation

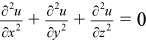
in a parallelepiped a_x< x < b_x , a_y< y < b_y, a_z< z < b_z with the Dirichlet, Neumann, or periodic boundary conditions on each boundary bd_+.

Approximation of 3D problems

To find an approximate solution for each of the 3D problems, a uniform mesh can be defined in the parallelepiped domain as:

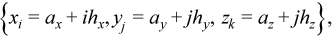
where

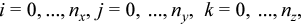
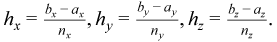
The Poisson Solver uses the standard seven-point finite difference approximation on this mesh to compute the approximation to the solution. The values of the approximate solution will be computed in the mesh points (x_i, y_j, z_k), provided that you can supply the values of the right-hand side f(x, y, z) in these points and the values of the appropriate boundary functions G(x, y, z) and/or g(x, y, z) in the mesh points laying on the boundary of the parallelepiped domain.

Parent topic: Fast Poisson Solver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

Poisson Solver Implementation

Two-Dimensional Problems

Three-Dimensional Problems