?getrf2

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-04EB4C92-B11E-4BA0-898A-E239C2B5C5E8

View Details

?getrf2

Computes LU factorization using partial pivoting with row interchanges.

Syntax

lapack_int LAPACKE_sgetrf2 (int matrix_layout, lapack_int m, lapack_int n, float * a, lapack_int lda, lapack_int * ipiv);

lapack_int LAPACKE_dgetrf2 (int matrix_layout, lapack_int m, lapack_int n, double * a, lapack_int lda, lapack_int * ipiv);

lapack_int LAPACKE_cgetrf2 (int matrix_layout, lapack_int m, lapack_int n, lapack_complex_float * a, lapack_int lda, lapack_int * ipiv);

lapack_int LAPACKE_zgetrf2 (int matrix_layout, lapack_int m, lapack_int n, lapack_complex_double * a, lapack_int lda, lapack_int * ipiv);

Include Files

mkl.h

Description

?getrf2 computes an LU factorization of a general m-by-n matrix A using partial pivoting with row interchanges.

The factorization has the form

A = P * L * U

where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n).

This is the recursive version of the algorithm. It divides the matrix into four submatrices:

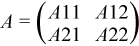
where A11 is n1 by n1 and A22 is n2 by n2 with n1 = min(m, n), and n2 = n - n1.

The subroutine calls itself to factor ,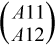

do the swaps on 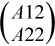, solve A12, update A22, then it calls itself to factor A22 and do the swaps on A21.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

m

The number of rows of the matrix A. m >= 0.

n

The number of columns of the matrix A. n >= 0.

a

Array, size lda*n.

On entry, the m-by-n matrix to be factored.

lda

The leading dimension of the array a. lda >= max(1,m).

Output Parameters

On exit, the factors L and U from the factorization A = P * L * U; the unit diagonal elements of L are not stored.

ipiv

Array, size (min(m,n)).

The pivot indices; for 1 <= i <= min(m,n), row i of the matrix was interchanged with row ipiv[i - 1].

Return Values

This function returns a value info.

= 0: successful exit

< 0: if info = -i, the i-th argument had an illegal value.

> 0: if info = i, U_{i, i} is exactly zero. The factorization has been completed, but the factor U is exactly singular, and division by zero will occur if it is used to solve a system of equations.

Parent topic: Matrix Factorization: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?getrf2

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values