?ggglm

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-F8E62707-AACE-491E-B783-C502B870C397

View Details

?ggglm

Solves a general Gauss-Markov linear model problem using a generalized QR factorization.

Syntax

lapack_int LAPACKE_sggglm (int matrix_layout, lapack_int n, lapack_int m, lapack_int p, float* a, lapack_int lda, float* b, lapack_int ldb, float* d, float* x, float* y);

lapack_int LAPACKE_dggglm (int matrix_layout, lapack_int n, lapack_int m, lapack_int p, double* a, lapack_int lda, double* b, lapack_int ldb, double* d, double* x, double* y);

lapack_int LAPACKE_cggglm (int matrix_layout, lapack_int n, lapack_int m, lapack_int p, lapack_complex_float* a, lapack_int lda, lapack_complex_float* b, lapack_int ldb, lapack_complex_float* d, lapack_complex_float* x, lapack_complex_float* y);

lapack_int LAPACKE_zggglm (int matrix_layout, lapack_int n, lapack_int m, lapack_int p, lapack_complex_double* a, lapack_int lda, lapack_complex_double* b, lapack_int ldb, lapack_complex_double* d, lapack_complex_double* x, lapack_complex_double* y);

Include Files

mkl.h

Description

The routine solves a general Gauss-Markov linear model (GLM) problem:

minimize_x ||y||₂ subject to d = A*x + B*y

where A is an n-by-m matrix, B is an n-by-p matrix, and d is a given n-vector. It is assumed that m≤n≤m+p, and rank(A) = m and rank(AB) = n.

Under these assumptions, the constrained equation is always consistent, and there is a unique solution x and a minimal 2-norm solution y, which is obtained using a generalized QR factorization of the matrices (A, B ) given by

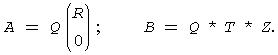
In particular, if matrix B is square nonsingular, then the problem GLM is equivalent to the following weighted linear least squares problem

minimize_x ||B^-1(d-A*x)||₂.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

n

The number of rows of the matrices A and B (n≥ 0).

m

The number of columns in A (m≥ 0).

p

The number of columns in B (p≥n - m).

a, b, d

Arrays:

a(size max(1, lda*m) for column major layout and max(1, lda*n) for row major layout) contains the n-by-m matrix A.

b(size max(1, ldb*p) for column major layout and max(1, ldb*n) for row major layout) contains the n-by-p matrix B.

d, size at least max(1, n), contains the left hand side of the GLM equation.

lda

The leading dimension of a; at least max(1, n)for column major layout and max(1, m) for row major layout.

ldb

The leading dimension of b; at least max(1, n)for column major layout and max(1, p) for row major layout.

Output Parameters

x, y

Arrays x, y. size at least max(1, m) for x and at least max(1, p) for y.

On exit, x and y are the solutions of the GLM problem.

a

On exit, the upper triangular part of the array a contains the m-by-m upper triangular matrix R.

b

On exit, if n ≤ p, the upper right triangle contains the n-by-n upper triangular matrix T as returned by ?ggrqf; if n > p, the elements on and above the (n-p)-th subdiagonal contain the n-by-p upper trapezoidal matrix T.

d

On exit, d is destroyed

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = 1, the upper triangular factor R associated with A in the generalized QR factorization of the pair (A, B) is singular, so that rank(A) < m; the least squares solution could not be computed.

If info = 2, the bottom (n-m)-by-(n-m) part of the upper trapezoidal factor T associated with B in the generalized QR factorization of the pair (A, B) is singular, so that rank(AB) < n; the least squares solution could not be computed.

Parent topic: Generalized Linear Least Squares (LLS) Problems: LAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?ggglm

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values