?unghr

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-3D274DD7-1977-4DB7-B39F-DCEC320D3435

View Details

?unghr

Generates the complex unitary matrix Q determined by ?gehrd.

Syntax

call cunghr(n, ilo, ihi, a, lda, tau, work, lwork, info)

call zunghr(n, ilo, ihi, a, lda, tau, work, lwork, info)

call unghr(a, tau [,ilo] [,ihi] [,info])

Include Files

mkl.fi, lapack.f90

Description

The routine is intended to be used following a call to cgehrd/zgehrd, which reduces a complex matrix A to upper Hessenberg form H by a unitary similarity transformation: A = Q*H*Q^H. ?gehrd represents the matrix Q as a product of ihi-iloelementary reflectors. Here ilo and ihi are values determined by cgebal/zgebal when balancing the matrix; if the matrix has not been balanced, ilo = 1 and ihi = n.

Use the routine unghr to generate Q explicitly as a square matrix. The matrix Q has the structure:

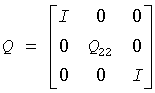
where Q₂₂ occupies rows and columns ilo to ihi.

Input Parameters

n

INTEGER. The order of the matrix Q (n≥ 0).

ilo, ihi

INTEGER. These must be the same parameters ilo and ihi, respectively, as supplied to ?gehrd . (If n > 0, then 1 ≤ilo≤ihi≤n. If n = 0, then ilo = 1 and ihi = 0.)

a, tau, work

COMPLEX for cunghr

DOUBLE COMPLEX for zunghr.

Arrays:

a(lda,*) contains details of the vectors which define the elementary reflectors, as returned by ?gehrd.

The second dimension of a must be at least max(1, n).

tau(*) contains further details of the elementary reflectors, as returned by ?gehrd .

The dimension of tau must be at least max (1, n-1).

work is a workspace array, its dimension max(1, lwork).

lda

INTEGER. The leading dimension of a; at least max(1, n).

lwork

INTEGER. The size of the work array;

lwork≥ max(1, ihi-ilo).

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla.

See Application Notes for the suggested value of lwork.

Output Parameters

a

Overwritten by the n-by-n unitary matrix Q.

work(1)

If info = 0, on exit work(1) contains the minimum value of lwork required for optimum performance. Use this lwork for subsequent runs.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine unghr interface are the following:

a: Holds the matrix A of size (n,n).
tau: Holds the vector of length (n-1).
ilo: Default value for this argument is ilo = 1.
ihi: Default value for this argument is ihi = n.

Application Notes

For better performance, try using lwork = (ihi-ilo)*blocksize, where blocksize is a machine-dependent value (typically, 16 to 64) required for optimum performance of the blocked algorithm.

If it is not clear how much workspace to supply, use a generous value of lwork for the first run, or set lwork = -1.

In first case the routine completes the task, though probably not so fast as with a recommended workspace, and provides the recommended workspace in the first element of the corresponding array work on exit. Use this value (work(1)) for subsequent runs.

If lwork = -1, then the routine returns immediately and provides the recommended workspace in the first element of the corresponding array (work). This operation is called a workspace query.

Note that if lwork is less than the minimal required value and is not equal to -1, then the routine returns immediately with an error exit and does not provide any information on the recommended workspace.

The computed matrix Q differs from the exact result by a matrix E such that ||E||₂ = O(ε), where ε is the machine precision.

The approximate number of real floating-point operations is (16/3)(ihi-ilo)³.

The real counterpart of this routine is orghr.

Parent topic: Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?unghr

Syntax

Include Files

Description

Input Parameters

Output Parameters

LAPACK 95 Interface Notes

Application Notes