p?gecon

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-168B4B45-834B-46D8-BB8E-239403DD6BD5

View Details

p?gecon

Estimates the reciprocal of the condition number of a general distributed matrix in either the 1-norm or the infinity-norm.

Syntax

call psgecon(norm, n, a, ia, ja, desca, anorm, rcond, work, lwork, iwork, liwork, info)

call pdgecon(norm, n, a, ia, ja, desca, anorm, rcond, work, lwork, iwork, liwork, info)

call pcgecon(norm, n, a, ia, ja, desca, anorm, rcond, work, lwork, rwork, lrwork, info)

call pzgecon(norm, n, a, ia, ja, desca, anorm, rcond, work, lwork, rwork, lrwork, info)

Include Files

Description

The p?gecon routine estimates the reciprocal of the condition number of a general distributed real/complex matrix sub(A) = A(ia:ia+n-1, ja:ja+n-1) in either the 1-norm or infinity-norm, using the LU factorization computed by p?getrf.

An estimate is obtained for ||(sub(A))^-1||, and the reciprocal of the condition number is computed as

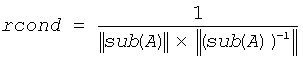
Input Parameters

norm

(global) CHARACTER*1. Must be '1' or 'O' or 'I'.

Specifies whether the 1-norm condition number or the infinity-norm condition number is required.

If norm = '1' or 'O', then the 1-norm is used;

If norm = 'I', then the infinity-norm is used.

n

(global) INTEGER. The order of the distributed matrix sub(A) (n≥ 0).

a

(local)

REAL for psgecon

DOUBLE PRECISION for pdgecon

COMPLEX for pcgecon

DOUBLE COMPLEX for pzgecon.

Pointer into the local memory to an array of size (lld_a,LOCc(ja+n-1)).

The array a contains the local pieces of the factors L and U from the factorization sub(A) = P*L*U; the unit diagonal elements of L are not stored.

ia, ja

(global) INTEGER. The row and column indices in the global matrix A indicating the first row and the first column of the matrix sub(A), respectively.

desca

(global and local) INTEGER array of size dlen_. The array descriptor for the distributed matrix A.

anorm

(global) REAL for single precision flavors, DOUBLE PRECISION for double precision flavors.

If norm = '1' or 'O', the 1-norm of the original distributed matrix sub(A);

If norm = 'I', the infinity-norm of the original distributed matrix sub(A).

work

(local)

REAL for psgecon

DOUBLE PRECISION for pdgecon

COMPLEX for pcgecon

DOUBLE COMPLEX for pzgecon.

The array work of size lwork is a workspace array.

lwork

(local or global) INTEGER. The size of the array work.

For real flavors:

lwork must be at least

lwork≥ 2*LOCr(n+mod(ia-1,mb_a))+2*LOCc(n+mod(ja-1,nb_a))+max(2, max(nb_a*max(1, iceil(NPROW-1, NPCOL)), LOCc(n+mod(ja-1,nb_a)) + nb_a*max(1, iceil(NPCOL-1, NPROW)))).

For complex flavors:

lwork must be at least

lwork≥ 2*LOCr(n+mod(ia-1,mb_a))+max(2, max(nb_a*iceil(NPROW-1, NPCOL), LOCc(n+mod(ja-1,nb_a))+ nb_a*iceil(NPCOL-1, NPROW))).

LOCr and LOCc values can be computed using the ScaLAPACK tool function numroc; NPROW and NPCOL can be determined by calling the subroutine blacs_gridinfo.

NOTE:

iceil(x,y) is the ceiling of x/y, and mod(x,y) is the integer remainder of x/y.

iwork

(local) INTEGER. Workspace array of size liwork. Used in real flavors only.

liwork

(local or global) INTEGER. The size of the array iwork; used in real flavors only. Must be at least

liwork≥LOCr(n+mod(ia-1,mb_a)).

rwork

(local) REAL for pcgecon

DOUBLE PRECISION for pzgecon

Workspace array of size lrwork. Used in complex flavors only.

lrwork

(local or global) INTEGER. The size of the array rwork; used in complex flavors only. Must be at least

lrwork≥ max(1, 2*LOCc(n+mod(ja-1,nb_a))).

Output Parameters

rcond

(global) REAL for single precision flavors.

DOUBLE PRECISION for double precision flavors.

The reciprocal of the condition number of the distributed matrix sub(A). See Description.

work(1)

On exit, work(1) contains the minimum value of lwork required for optimum performance.

iwork(1)

On exit, iwork(1) contains the minimum value of liwork required for optimum performance (for real flavors).

rwork(1)

On exit, rwork(1) contains the minimum value of lrwork required for optimum performance (for complex flavors).

info

(global) INTEGER. If info=0, the execution is successful.

info < 0:

If the i-th argument is an array and the j-th entry had an illegal value, then info = -(i*100+j); if the i-th argument is a scalar and had an illegal value, then info = -i.

Parent topic: Estimating the Condition Number: ScaLAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

p?gecon

Syntax

Include Files

Description

Input Parameters

Output Parameters

See Also