?orm22/?unm22

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-B04220A7-9433-439E-A839-C7360F15DFA1

View Details

?orm22/?unm22

Multiplies a general matrix by an orthogonal/unitary matrix with a 2x2 structure.

Syntax

call sorm22 (side, trans, m, n, n1, n2, q, ldq, c, ldc, work, lwork, info )

call dorm22 (side, trans, m, n, n1, n2, q, ldq, c, ldc, work, lwork, info )

call cunm22(side, trans, m, n, n1, n2, q, ldq, c, ldc, work, lwork, info)

call zunm22(side, trans, m, n, n1, n2, q, ldq, c, ldc, work, lwork, info)

Include Files

mkl.fi

Description

?orm22/?unm22 overwrites the general real/complex m-by-n matrix C with

	side = 'L'	side = 'R'
trans = 'N'	`Q` * `C`	`C` * `Q`
trans = 'T' applies to sorm22 and dorm22 only	`Q`^T * `C`	`C` * `Q`^T
trans = 'C' applies to cunm22 and zunm22 only	`Q`^H * `C`	`C` * `Q`^H

where Q is a real orthogonal/complex unitary matrix of order nq, with nq = m if side = 'L' and nq = n if side = 'R'.

The orthogonal/unitary matrix Q processes a 2-by-2 block structure:

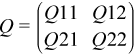
where Q12 is an n1-by-n1 lower triangular matrix and Q21 is an n2-by-n2 upper triangular matrix.

Input Parameters

side

CHARACTER*1. = 'L': apply Q, Q^T, or Q^H from the left;

= 'R': apply Q, Q^T, or Q^H from the right.

trans

CHARACTER*1. = 'N': apply Q (no transpose);

= 'T': apply Q^T (transpose) - sorm22 and dorm22 only;

= 'C': apply Q^H (conjugate transpose) - cunm22 and zunm22 only.

m

INTEGER. The number of rows of the matrix C.

m≥ 0.

n

INTEGER. The number of columns of the matrix C.

n≥ 0.

n1

INTEGER. The dimension of Q12.

n1≥ 0.

The following requirement must be satisfied: n1 + n2 = m if side = 'L' and n1 + n2 = n if side = 'R'.

n2

INTEGER. The dimension of Q21.

n2≥ 0.

The following requirement must be satisfied: n1 + n2 = m if side = 'L' and n1 + n2 = n if side = 'R'.

q

REAL for sorm22

DOUBLE PRECISION for dorm22

COMPLEX for cunm22

DOUBLE COMPLEX for zunm22

Array, size (ldq,m) if side = 'L' and (ldq,n) if side = 'R'.

ldq

INTEGER. The leading dimension of the array q.

ldq≥ max(1,m) if side = 'L';

ldq≥ max(1,n) if side = 'R'.

c

REAL for sorm22

DOUBLE PRECISION for dorm22

COMPLEX for cunm22

DOUBLE COMPLEX for zunm22

Array, size (ldc,n)

On entry, the m-by-n matrix C.

ldc

INTEGER. The leading dimension of the array c.

ldc≥ max(1,m).

lwork

INTEGER. The dimension of the array work.

If side = 'L', lwork≥ max(1,n);

if side = 'R', lwork≥ max(1,m).

For optimum performance lwork≥m*n.

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla.

Output Parameters

On exit, c is overwritten by the product:

Q*C,

Q^T*C,

Q^H * C,

C*Q^T,

C * Q^H, or

C*Q.

work

REAL for sorm22

DOUBLE PRECISION for dorm22

COMPLEX for cunm22

DOUBLE COMPLEX for zunm22

Array, size (max(1,lwork))

On exit, if info = 0, work(1) returns the optimal lwork.

info

INTEGER. = 0: successful exit.

< 0: if info = -i, the i-th argument had an illegal value.

Parent topic: Symmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?orm22/?unm22

Syntax

Include Files

Description

Input Parameters

Output Parameters