?orcsd2by1/?uncsd2by1

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-B0D954D3-95F7-4081-9496-86A79506C2BE

View Details

?orcsd2by1/?uncsd2by1

Computes the CS decomposition of a block-partitioned orthogonal/unitary matrix.

Syntax

call sorcsd2by1( jobu1, jobu2, jobv1t, m, p, q, x11, ldx11, x21, ldx21, theta, u1, ldu1, u2, ldu2, v1t, ldv1t, work, lwork, iwork, info )

call dorcsd2by1( jobu1, jobu2, jobv1t, m, p, q, x11, ldx11, x21, ldx21, theta, u1, ldu1, u2, ldu2, v1t, ldv1t, work, lwork, iwork, info )

call cuncsd2by1( jobu1, jobu2, jobv1t, m, p, q, x11, ldx11, x21, ldx21, theta, u1, ldu1, u2, ldu2, v1t, ldv1t, work, lwork, rwork, lrwork, iwork, info )

call zuncsd2by1( jobu1, jobu2, jobv1t, m, p, q, x11, ldx11, x21, ldx21, theta, u1, ldu1, u2, ldu2, v1t, ldv1t, work, lwork, rwork, lrwork, iwork, info )

call orcsd2by1( x11,x21,theta,u1,u2,v1t[,jobu1][,jobu2][,jobv1t][,info] )

call uncsd2by1( x11,x21,theta,u1,u2,v1t[,jobu1][,jobu2][,jobv1t][,info] )

Include Files

mkl.fi, lapack.f90

Description

The routines ?orcsd2by1/?uncsd2by1 compute the CS decomposition of an m-by-q matrix X with orthonormal columns that has been partitioned into a 2-by-1 block structure:

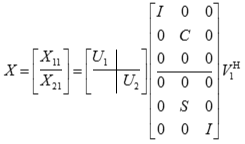
x₁₁ is p-by-q. The orthogonal/unitary matrices u₁, u₂, v₁, and v₂ are p-by-p, (m-p)-by-(m-p), q-by-q, (m-q)-by-(m-q), respectively. C and S are r-by-r nonnegative diagonal matrices satisfying C² + S² = I, in which r = min(p,m-p,q,m-q).

Input Parameters

jobu1

CHARACTER. If equal to 'Y', then u₁ is computed. Otherwise, u₁ is not computed.

jobu2

CHARACTER. If equal to 'Y', then u₂ is computed. Otherwise, u₂ is not computed.

jobv1t

CHARACTER. If equal to 'Y', then v₁^t is computed. Otherwise, v₁^t is not computed.

m

INTEGER. The number of rows and columns of the matrix X.

p

INTEGER. The number of rows in x₁₁. 0 ≤p≤m.

q

INTEGER. The number of columns in x₁₁ . 0 ≤q≤m.

x11

REAL for sorcsd2by1

DOUBLE PRECISION for dorcsd2by1

COMPLEX for cuncsd2by1

DOUBLE COMPLEX for zuncsd2by1

Array, size (ldx11,q).

On entry, the part of the orthogonal matrix whose CSD is desired.

ldx11

INTEGER. The leading dimension of the array x11. ldx11≥ max(1,p).

x21

REAL for sorcsd2by1

DOUBLE PRECISION for dorcsd2by1

COMPLEX for cuncsd2by1

DOUBLE COMPLEX for zuncsd2by1

Array, size (ldx21,q).

On entry, the part of the orthogonal matrix whose CSD is desired.

ldx21

INTEGER. The leading dimension of the array X. ldx21≥ max(1,m - p).

ldu1

INTEGER. The leading dimension of the array u₁. If jobu1 = 'Y', ldu1≥ max(1,p).

ldu2

INTEGER. The leading dimension of the array u₂. If jobu2 = 'Y', ldu2≥ max(1,m-p).

ldv1t

INTEGER. The leading dimension of the array v1t. If jobv1t = 'Y', ldv1t≥ max(1,q).

work

REAL for sorcsd2by1

DOUBLE PRECISION for dorcsd2by1

COMPLEX for cuncsd2by1

DOUBLE COMPLEX for zuncsd2by1

Workspace array, size (max(1,lwork)).

lwork

INTEGER. The size of the work array. Constraints:

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla.

rwork

REAL for cuncsd2by1

DOUBLE PRECISION for zuncsd2by1

Workspace array, size (max(1,lrwork)).

lrwork

INTEGER. The size of the rwork array. Constraints:

If lrwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the rwork array, returns this value as the first entry of the rwork array, and no error message related to lrwork is issued by xerbla.

iwork

INTEGER. Workspace array, dimension m - min(p, m - p, q, m - q).

Output Parameters

theta

REAL for sorcsd2by1

DOUBLE PRECISION for dorcsd2by1

COMPLEX for cuncsd2by1

DOUBLE COMPLEX for zuncsd2by1

Array, size (r), in which r = min(p,m-p,q,m-q).

C = diag( cos(theta(1)), ..., cos(theta(r)) ), and

S = diag( sin(theta(1)), ..., sin(theta(r)) ).

u1

REAL for sorcsd2by1

DOUBLE PRECISION for dorcsd2by1

COMPLEX for cuncsd2by1

DOUBLE COMPLEX for zuncsd2by1

Array, size (ldu1,p) .

If jobu1 = 'Y', u1 contains the p-by-p orthogonal/unitary matrix u₁.

u2

REAL for sorcsd2by1

DOUBLE PRECISION for dorcsd2by1

COMPLEX for cuncsd2by1

DOUBLE COMPLEX for zuncsd2by1

Array, size (ldu2,m - p) .

If jobu2 = 'Y', u2 contains the (m-p)-by-(m-p) orthogonal/unitary matrix u₂.

v1t

REAL for sorcsd2by1

DOUBLE PRECISION for dorcsd2by1

COMPLEX for cuncsd2by1

DOUBLE COMPLEX for zuncsd2by1

Array, size (ldv1t,q) .

If jobv1t = 'Y', v1t contains the q-by-q orthogonal matrix v₁^T or unitary matrix v₁^H.

work

On exit,

If info = 0,: work(1) returns the optimal lwork.
If info > 0,: work(2:r) contains the values phi(1), ..., phi(r-1) that, together with theta(1), ..., theta(r) define the matrix in intermediate bidiagonal-block form remaining after nonconvergence. info specifies the number of nonzero phi's.

rwork

On exit,

If info = 0,: rwork(1) returns the optimal lrwork.
If info > 0,: rwork(2:r) contains the values phi(1), ..., phi(r-1) that, together with theta(1), ..., theta(r) define the matrix in intermediate bidiagonal-block form remaining after nonconvergence. info specifies the number of nonzero phi's.

info

INTEGER.

= 0: successful exit

< 0: if info = -i, the i-th argument has an illegal value

> 0: ?orcsd2by1/?uncsd2by1 did not converge. See the description of work above for details.

Fortran 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or reconstructible arguments, see Fortran 95 Interface Conventions.

Specific details for the routine ?orcsd2by1/?orcsd2by1 interface are as follows:

x11: Holds the block of matrix X₁₁ of size (p, q).
x21: Holds the block of matrix X₂₁ of size (m-p, q).
theta: Holds the vector of length r = min(p,m-p,q,m-q).
u1: Holds the matrix u₁ of size (p,p).
u2: Holds the matrix u₂ of size (m-p,m-p).
v1t: Holds the matrix v₁^T or v₁^H of size (q,q).
jobu1: Indicates whether u₁ is computed. Must be 'Y' or 'O'.
jobu2: Indicates whether u₂ is computed. Must be 'Y' or 'O'.
jobv1t: Indicates whether v₁^t is computed. Must be 'Y' or 'O'.

Parent topic: Cosine-Sine Decomposition: LAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?orcsd2by1/?uncsd2by1

Syntax

Include Files

Description

Input Parameters

Output Parameters

Fortran 95 Interface Notes

See Also