?dbtf2

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-FC424856-C9FD-4531-9140-4CF7D1C23BD8

View Details

?dbtf2

Computes an LU factorization of a general band matrix with no pivoting (local unblocked algorithm).

Syntax

call sdbtf2(m, n, kl, ku, ab, ldab, info)

call ddbtf2(m, n, kl, ku, ab, ldab, info)

call cdbtf2(m, n, kl, ku, ab, ldab, info)

call zdbtf2(m, n, kl, ku, ab, ldab, info)

Description

The ?dbtf2routine computes an LU factorization of a general real/complex m-by-n band matrix A without using partial pivoting with row interchanges.

This is the unblocked version of the algorithm, calling BLAS Routines and Functions.

Input Parameters

m

INTEGER. The number of rows of the matrix A(m ≥ 0).

n

INTEGER. The number of columns in A(n ≥ 0).

kl

INTEGER. The number of sub-diagonals within the band of A(kl ≥ 0).

ku

INTEGER. The number of super-diagonals within the band of A(ku ≥ 0).

ab

REAL for sdbtf2

DOUBLE PRECISION for ddbtf2

COMPLEX for cdbtf2

COMPLEX*16 for zdbtf2.

Array of size ldab by n.

The matrix A in band storage, in rows kl+1 to 2kl+ku+1; rows 1 to kl of the array need not be set. The j-th column of A is stored in thej-th column of the array ab as follows: ab(kl+ku+1+i-j,j) = A(i,j) for max(1,j-ku) ≤ i ≤ min(m,j+kl).

ldab

INTEGER. The leading dimension of the array ab.

(ldab ≥ 2kl + ku +1)

Output Parameters

ab

On exit, details of the factorization: U is stored as an upper triangular band matrix with kl+ku superdiagonals in rows 1 to kl+ku+1, and the multipliers used during the factorization are stored in rows kl+ku+2 to 2*kl+ku+1. See the Application Notes below for further details.

info

INTEGER.

= 0: successful exit

< 0: if info = - i, the i-th argument had an illegal value,

> 0: if info = + i, U(i,i) is 0. The factorization has been completed, but the factor U is exactly singular. Division by 0 will occur if you use the factor U for solving a system of linear equations.

Application Notes

The band storage scheme is illustrated by the following example, when m = n = 6, kl = 2, ku = 1:

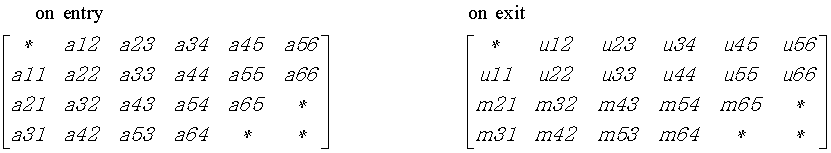
The routine does not use array elements marked *; elements marked + need not be set on entry, but the routine requires them to store elements of U, because of fill-in resulting from the row interchanges.

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?dbtf2

Syntax

Description

Input Parameters

Output Parameters

Application Notes

See Also