?gesvj

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-9469788C-1DF5-46A8-999B-F71B17245938

View Details

?gesvj

Computes the singular value decomposition of a real matrix using Jacobi plane rotations.

Syntax

call sgesvj(joba, jobu, jobv, m, n, a, lda, sva, mv, v, ldv, work, lwork, info)

call dgesvj(joba, jobu, jobv, m, n, a, lda, sva, mv, v, ldv, work, lwork, info)

call cgesvj(joba, jobu, jobv, m, n, a, lda, sva, mv, v, ldv, cwork, lwork, rwork, lrwork, info )

call zgesvj(joba, jobu, jobv, m, n, a, lda, sva, mv, v, ldv, cwork, lwork, rwork, lrwork, info )

Include Files

mkl.fi

Description

The routine computes the singular value decomposition (SVD) of a real or complex m-by-n matrix A, where m≥n.

The SVD of A is written as

A = U*Σ*V^T for real flavors, or

A = U*Σ*V^H for complex flavors,

where Σ is an m-by-n diagonal matrix, U is an m-by-n orthonormal matrix, and V is an n-by-n orthogonal/unitary matrix. The diagonal elements of Σ are the singular values of A; the columns of U and V are the left and right singular vectors of A, respectively. The matrices U and V are computed and stored in the arrays u and v, respectively. The diagonal of Σ is computed and stored in the array sva.

The ?gesvj routine can sometimes compute tiny singular values and their singular vectors much more accurately than other SVD routines.

The n-by-n orthogonal matrix V is obtained as a product of Jacobi plane rotations. The rotations are implemented as fast scaled rotations of Anda and Park [AndaPark94]. In the case of underflow of the Jacobi angle, a modified Jacobi transformation of Drmac ([Drmac08-4]) is used. Pivot strategy uses column interchanges of de Rijk ([deRijk98]). The relative accuracy of the computed singular values and the accuracy of the computed singular vectors (in angle metric) is as guaranteed by the theory of Demmel and Veselic [Demmel92]. The condition number that determines the accuracy in the full rank case is essentially

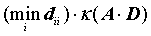
where κ(.) is the spectral condition number. The best performance of this Jacobi SVD procedure is achieved if used in an accelerated version of Drmac and Veselic [Drmac08-1], [Drmac08-2].

The computational range for the nonzero singular values is the machine number interval ( UNDERFLOW,OVERFLOW ). In extreme cases, even denormalized singular values can be computed with the corresponding gradual loss of accurate digit.

Input Parameters

joba

CHARACTER*1. Must be 'L', 'U' or 'G'.

Specifies the structure of A:

If joba = 'L', the input matrix A is lower triangular.

If joba = 'U', the input matrix A is upper triangular.

If joba = 'G', the input matrix A is a general m-by-n, m≥n.

jobu

CHARACTER*1. Must be 'U', 'C' or 'N'.

Specifies whether to compute the left singular vectors (columns of U):

If jobu = 'U', the left singular vectors corresponding to the nonzero singular values are computed and returned in the leading columns of A. See more details in the description of a. The default numerical orthogonality threshold is set to approximately TOL=CTOL*EPS, CTOL=sqrt(m), EPS = ?lamch('E')

If jobu = 'C', analogous to jobu = 'U', except that you can control the level of numerical orthogonality of the computed left singular vectors. TOL can be set to TOL=CTOL*EPS, where CTOL is given on input in the array work. No CTOL smaller than ONE is allowed. CTOL greater than 1 / EPS is meaningless. The option 'C' can be used if m*EPS is satisfactory orthogonality of the computed left singular vectors, so CTOL=m could save a few sweeps of Jacobi rotations. See the descriptions of a and work(1).

If jobu = 'N', u is not computed. However, see the description of a.

jobv

CHARACTER*1. Must be 'V', 'A' or 'N'.

Specifies whether to compute the right singular vectors, that is, the matrix V:

If jobv = 'V', the matrix V is computed and returned in the array v.

If jobv = 'A', the Jacobi rotations are applied to the mv-byn array v. In other words, the right singular vector matrix V is not computed explicitly, instead it is applied to an mv-byn matrix initially stored in the first mv rows of V.

If jobv = 'N', the matrix V is not computed and the array v is not referenced.

m

INTEGER. The number of rows of the input matrix A.

1/slamch('E')> m≥ 0 for sgesvj.

1/dlamch('E')> m≥ 0 for dgesvj.

n

INTEGER. The number of columns in the input matrix A; m≥n≥ 0.

a, v

REAL for sgesvj

DOUBLE PRECISION for dgesvj.

COMPLEX for cgesvj

DOUBLE COMPLEX for zgesvj

Array a(lda,n) is an array containing the m-by-n matrix A.

Array v is a workspace array, its dimension is (ldv,*); the second dimension of v must be at least max(1, n).

lda

INTEGER. The leading dimension of the array a. Must be at least max(1, m) .

mv

INTEGER.

Ifjobv = 'A', the product of Jacobi rotations in ?gesvj is applied to the first mv rows of v. See the description of jobv. 0 ≤mv≤ldv.

ldv

INTEGER. The leading dimension of the array v; ldv≥ 1.

jobv = 'V', ldv≥ max(1, n).

jobv = 'A', ldv≥ max(1, mv).

work

REAL for sgesvj

DOUBLE PRECISION for dgesvj.

work is a workspace array, its dimension max(4, m+n).

If jobu = 'C', work(1)=CTOL, where CTOL defines the threshold for convergence. The process stops if all columns of A are mutually orthogonal up to CTOL*EPS, EPS=?lamch('E'). It is required that CTOL ≥ 1, that is, it is not allowed to force the routine to obtain orthogonality below ε.

cwork

COMPLEX for cgesvj

DOUBLE COMPLEX for zgesvj

cwork is a workspace array, its dimension m+n.

lwork

INTEGER.

Length of work for real flavors or cwork for complex flavors, lwork≥ max(6,m+n).

rwork

REAL for cgesvj

DOUBLE PRECISION for zgesvj

rwork is a workspace array, its dimension max(6,m+n).

If jobu = 'C', rwork(1) = CTOL, where CTOL defines the threshold for convergence. The process stops if all columns of a are mutually orthogonal up to CTOL*EPS, EPS=?lamch('E'). It is required that CTOL≥ 1, that is, it is not allowed to force the routine to obtain orthogonality below ε.

lrwork

INTEGER for cgesvj

INTEGER for zgesvj

Length of rwork, lrwork≥ max(6,n).

Output Parameters

a

On exit:

If jobu = 'U' or jobu = 'C':

if info = 0, the leading columns of A contain left singular vectors corresponding to the computed singular values of a that are above the underflow threshold ?lamch('S'), that is, non-zero singular values. The number of the computed non-zero singular values is returned in work(2) for real flavors or rwork(2) for complex flavors. Also see the descriptions of sva and work for real flavors or rwork for complex flavors. The computed columns of u are mutually numerically orthogonal up to approximately TOL=sqrt(m)*EPS (default); or TOL=CTOL*EPSjobu = 'C', see the description of jobu.
if info > 0, the procedure ?gesvj did not converge in the given number of iterations (sweeps). In that case, the computed columns of u may not be orthogonal up to TOL. The output u (stored in a), sigma (given by the computed singular values in sva(1:n)) and v is still a decomposition of the input matrix A in the sense that the residual ||A-scale*U*sigma*V^T||₂ / ||A||₂ for real flavors or ||A-scale*U*sigma*V^H||₂ / ||A||₂ for complex flavors (where scale = stat[0]) is small.

If jobu = 'N':

if info = 0, note that the left singular vectors are 'for free' in the one-sided Jacobi SVD algorithm. However, if only the singular values are needed, the level of numerical orthogonality of u is not an issue and iterations are stopped when the columns of the iterated matrix are numerically orthogonal up to approximately m*EPS. Thus, on exit, a contains the columns of u scaled with the corresponding singular values.
if info > 0, the procedure ?gesvj did not converge in the given number of iterations (sweeps).

sva

REAL for sgesvj

DOUBLE PRECISION for dgesvj.

REAL for cgesvj

DOUBLE PRECISION for zgesvj

Array size n.

If info = 0, depending on the value scale =work(1) for real flavors or rwork(1) for complex flavors, where scale is the scaling factor:

if scale = 1, sva(1:n) contains the computed singular values of a.

During the computation, sva contains the Euclidean column norms of the iterated matrices in the array a.
if scale≠ 1, the singular values of a are scale*sva(1:n), and this factored representation is due to the fact that some of the singular values of a might underflow or overflow.

If info > 0, the procedure ?gesvj did not converge in the given number of iterations (sweeps) and scale*sva(1:n) may not be accurate.

v

On exit:

If jobv = 'V', contains the n-by-n matrix of the right singular vectors.

If jobv = 'A', then v contains the product of the computed right singular vector matrix and the initial matrix in the array v.

If jobv = 'N', v is not referenced.

work

On exit,

work(1) = scale is the scaling factor such that scale*sva(1:n) are the computed singular values of A. See the description of sva().

work(2) is the number of the computed nonzero singular values.

work(3) is the number of the computed singular values that are larger than the underflow threshold.

work(4) is the number of sweeps of Jacobi rotations needed for numerical convergence.

work(5) = max_{i≠j} |COS(A(:,i),A(:,j))| in the last sweep. This is useful information in cases when ?gesvj did not converge, as it can be used to estimate whether the output is still useful and for post festum analysis.

work(6) is the largest absolute value over all sines of the Jacobi rotation angles in the last sweep. It can be useful in a post festum analysis.

rwork

On exit,

rwork(1) = scale is the scaling factor such that scale*sva(1:n) are the computed singular values of A. See description of sva().

rwork(2) is the number of the computed nonzero singular values.

rwork(3) is the number of the computed singular values that are larger than the underflow threshold.

rwork(4) is the number of sweeps of Jacobi rotations needed for numerical convergence.

rwork(5) = max_{i≠j} |COS(A(:,i),A(:,j))| in the last sweep. This is useful information in cases when ?gesvj did not converge, as it can be used to estimate whether the output is still useful and for post festum analysis.

rwork(6) is the largest absolute value over all sines of the Jacobi rotation angles in the last sweep. It can be useful for a post festum analysis.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info > 0, the function did not converge in the maximal number (30) of sweeps. The output may still be useful. See the description of work or rwork.

Parent topic: Singular Value Decomposition: LAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?gesvj

Syntax

Include Files

Description

Input Parameters

Output Parameters

See Also