?pbstf

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-9CD5CAD1-BECB-45C9-A917-F258038E127E

View Details

?pbstf

Computes a split Cholesky factorization of a real symmetric or complex Hermitian positive-definite banded matrix used in ?sbgst/?hbgst .

Syntax

call spbstf(uplo, n, kb, bb, ldbb, info)

call dpbstf(uplo, n, kb, bb, ldbb, info)

call cpbstf(uplo, n, kb, bb, ldbb, info)

call zpbstf(uplo, n, kb, bb, ldbb, info)

call pbstf(bb [, uplo] [,info])

Include Files

mkl.fi, lapack.f90

Description

The routine computes a split Cholesky factorization of a real symmetric or complex Hermitian positive-definite band matrix B. It is to be used in conjunction with sbgst/hbgst.

The factorization has the form B = S^T*S (or B = S^H*S for complex flavors), where S is a band matrix of the same bandwidth as B and the following structure: S is upper triangular in the first (n+kb)/2 rows and lower triangular in the remaining rows.

Input Parameters

uplo

CHARACTER*1. Must be 'U' or 'L'.

If uplo = 'U', bb stores the upper triangular part of B.

If uplo = 'L', bb stores the lower triangular part of B.

n

INTEGER. The order of the matrix B (n≥ 0).

kb

INTEGER. The number of super- or sub-diagonals in B

(kb≥ 0).

bb

REAL for spbstf

DOUBLE PRECISION for dpbstf

COMPLEX for cpbstf

DOUBLE COMPLEX for zpbstf.

bb(ldbb,*) is an array containing either upper or lower triangular part of the matrix B (as specified by uplo) in band storage format.

The second dimension of the array bb must be at least max(1, n).

ldbb

INTEGER. The leading dimension of bb; must be at least kb+1.

Output Parameters

bb

On exit, this array is overwritten by the elements of the split Cholesky factor S.

info

INTEGER.

If info = 0, the execution is successful.

If info = i, then the factorization could not be completed, because the updated element b_ii would be the square root of a negative number; hence the matrix B is not positive-definite.

If info = -i, the i-th parameter had an illegal value.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine pbstf interface are the following:

bb: Holds the array B of size (kb+1,n).
uplo: Must be 'U' or 'L'. The default value is 'U'.

Application Notes

The computed factor S is the exact factor of a perturbed matrix B + E, where

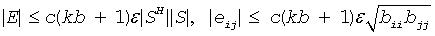
c(n) is a modest linear function of n, and ε is the machine precision.

The total number of floating-point operations for real flavors is approximately n(kb+1)². The number of operations for complex flavors is 4 times greater. All these estimates assume that kb is much less than n.

After calling this routine, you can call sbgst/hbgst to solve the generalized eigenproblem Az = λBz, where A and B are banded and B is positive-definite.

Parent topic: Generalized Symmetric-Definite Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?pbstf

Syntax

Include Files

Description

Input Parameters

Output Parameters

LAPACK 95 Interface Notes

Application Notes