?latm6

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-FB938B5D-8A07-4BBD-9595-2A42E80BCB7A

View Details

?latm6

Generates test matrices for the generalized eigenvalue problem, their corresponding right and left eigenvector matrices, and also reciprocal condition numbers for all eigenvalues and the reciprocal condition numbers of eigenvectors corresponding to the 1th and 5th eigenvalues.

Syntax

call slatm6( type, n, a, lda, b, x, ldx, y, ldy, alpha, beta, wx, wy, s, dif )

call dlatm6( type, n, a, lda, b, x, ldx, y, ldy, alpha, beta, wx, wy, s, dif )

call clatm6( type, n, a, lda, b, x, ldx, y, ldy, alpha, beta, wx, wy, s, dif )

call zlatm6( type, n, a, lda, b, x, ldx, y, ldy, alpha, beta, wx, wy, s, dif )

Include Files

mkl.fi

Description

The ?latm6 routine generates test matrices for the generalized eigenvalue problem, their corresponding right and left eigenvector matrices, and also reciprocal condition numbers for all eigenvalues and the reciprocal condition numbers of eigenvectors corresponding to the 1th and 5th eigenvalues.

There two kinds of test matrix pairs:

(A, B)= inverse(YH) * (Da, Db) * inverse(X)

Type 1:

Type 2:

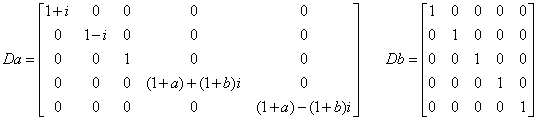
In both cases the same inverse(YH) and inverse(X) are used to compute (A, B), giving the exact eigenvectors to (A,B) as (YH, X):

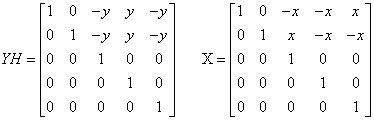where a, b, x and y will have all values independently of each other.

Input Parameters

type

INTEGER. Specifies the problem type.

n

INTEGER. Size of the matrices A and B.

lda

INTEGER. The leading dimension of a and of b.

ldx

INTEGER. The leading dimension of x.

ldy

INTEGER. The leading dimension of y.

alpha, beta

REAL for slatm6,

DOUBLE PRECISION for dlatm6,

COMPLEX for clatm6,

DOUBLE COMPLEX for zlatm6,

Weighting constants for matrix A.

wx

REAL for slatm6,

DOUBLE PRECISION for dlatm6,

COMPLEX for clatm6,

DOUBLE COMPLEX for zlatm6,

Constant for right eigenvector matrix.

wy

REAL for slatm6,

DOUBLE PRECISION for dlatm6,

COMPLEX for clatm6,

DOUBLE COMPLEX for zlatm6,

Constant for left eigenvector matrix.

Output Parameters

a

REAL for slatm6,

DOUBLE PRECISION for dlatm6,

COMPLEX for clatm6,

DOUBLE COMPLEX for zlatm6,

Array, size (lda, n). On exit, a contains the n-by-n matrix initialized according to type.

b

REAL for slatm26,

DOUBLE PRECISION for dlatm6,

COMPLEX for clatm6,

DOUBLE COMPLEX for zlatm6,

Array, size (lda, n). On exit, b contains the n-by-n matrix initialized according to type.

x

REAL for slatm6,

DOUBLE PRECISION for dlatm6,

COMPLEX for clatm6,

DOUBLE COMPLEX for zlatm6,

Array, size (ldx, n). On exit, x contains the n-by-n matrix of right eigenvectors.

y

REAL for slatm6,

DOUBLE PRECISION for dlatm6,

COMPLEX for clatm6,

DOUBLE COMPLEX for zlatm6,

Array, size (ldy, n). On exit, y is the n-by-n matrix of left eigenvectors.

s

REAL for slatm6,

DOUBLE PRECISION for dlatm6,

REAL for clatm6,

DOUBLE PRECISION for zlatm6,

Array, size (n). s(i ) is the reciprocal condition number for eigenvalue i .

dif

REAL for slatm6,

DOUBLE PRECISION for dlatm6,

REAL for clatm6,

DOUBLE PRECISION for zlatm6,

Array, size(n). dif(i ) is the reciprocal condition number for eigenvector i .

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?latm6

Syntax

Include Files

Description

Input Parameters

Output Parameters