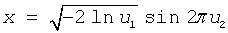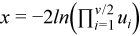Random Number Generators Naming Conventions

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-497D6D91-5031-4DCC-AE46-82B7EEF65AFE

View Details

Random Number Generators Naming Conventions

The names of the routines in VS random number generators are lowercase (virnguniform). The names are not case-sensitive.

The names of generator routines have the following structure:

v<type of result>rng<distribution>

where

v is the prefix of a VS vector function.
<type of result> is either s, d, or i and specifies one of the following types:

s

REAL

d

DOUBLE PRECISION

i

INTEGER

Prefixes s and d apply to continuous distributions only, prefix i applies only to discrete case.
rng indicates that the routine is a random generator.
<distribution> specifies the type of statistical distribution.

Names of service routines follow the template below:

vsl<name>

where

vsl is the prefix of a VS service function.
<name> contains a short function name.

For a more detailed description of service routines, refer to Service Routines and Advanced Service Routines.

The prototype of each generator routine corresponding to a given probability distribution fits the following structure:

status = <function name>( method, stream, n, r, [<distribution parameters>] )

where

method defines the method of generation. A detailed description of this parameter can be found in table "Values of <method> in method parameter". See below, where the structure of the method parameter name is explained.
stream defines the descriptor of the random stream and must have a non-zero value. Random streams, descriptors, and their usage are discussed further in Random Streams and Service Routines.
n defines the number of random values to be generated. If n is less than or equal to zero, no values are generated. Furthermore, if n is negative, an error condition is set.
r defines the destination array for the generated numbers. The dimension of the array must be large enough to store at least n random numbers.
status defines the error status of a VS routine. See Error Reporting for a detailed description of error status values.

Additional parameters included into <distribution parameters> field are individual for each generator routine and are described in detail in Distribution Generators.

To invoke a distribution generator, use a call to the respective VS routine. For example, to obtain a vector r, composed of n independent and identically distributed random numbers with normal (Gaussian) distribution, that have the mean value a and standard deviation sigma, write the following:

status = vsrnggaussian( method, stream, n, r, a, sigma )

The name of a method parameter has the following structure:

VSL_RNG_METHOD_method<distribution>_<method>

VSL_RNG_METHOD_<distribution>_<method>_ACCURATE

where

<distribution> is the probability distribution.
<method> is the method name.

Type of the name structure for the method parameter corresponds to fast and accurate modes of random number generation (see "Distribution Generators" and VS Notes for details).

Method names VSL_RNG_METHOD_<distribution>_<method>

and

VSL_RNG_METHOD_<distribution>_<method>_ACCURATE

should be used with

v<precision>Rng<distribution>

function only, where

<precision> is

s

for single precision continuous distribution

d

for double precision continuous distribution

i

for discrete distribution
<distribution> is the probability distribution.

is the probability distribution.Table "Values of <method> in method parameter" provides specific predefined values of the method name. The third column contains names of the functions that use the given method.

Values of `<method>` in method parameter
Method	Short Description	Functions
STD	Standard method. Currently there is only one method for these functions.	Uniform (continuous), Uniform (discrete), UniformBits, UniformBits32, UniformBits64
BOXMULLER	BOXMULLER generates normally distributed random number `x` thru the pair of uniformly distributed numbers `u`₁ and `u`₂ according to the formula:	Gaussian, GaussianMV
BOXMULLER2	BOXMULLER2 generates normally distributed random numbers `x`₁ and `x`₂ thru the pair of uniformly distributed numbers `u`₁ and `u`₂ according to the formulas:	Gaussian, GaussianMV, Lognormal
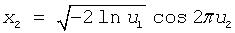
ICDF	Inverse cumulative distribution function method.	Exponential, Laplace, Weibull, Cauchy, Rayleigh, Gumbel, Bernoulli, Geometric, Gaussian, GaussianMV, Lognormal
GNORM	For α > 1, a gamma distributed random number is generated as a cube of properly scaled normal random number; for 0.6 ≤α < 1, a gamma distributed random number is generated using rejection from Weibull distribution; for α < 0.6, a gamma distributed random number is obtained using transformation of exponential power distribution; for α = 1, gamma distribution is reduced to exponential distribution.	Gamma
CJA	For `min(p, q) > 1`, Cheng method is used; for `min(p, q) < 1`, Johnk method is used, if `q + K·p²+ C≤ 0` (`K` = 0.852..., `C`=-0.956...) otherwise, Atkinson switching algorithm is used; for `max(p, q) < 1`, method of Johnk is used; for `min(p, q) < 1, max(p, q)> 1`, Atkinson switching algorithm is used (CJA stands for the first letters of Cheng, Johnk, Atkinson); for `p = 1` or `q = 1`, inverse cumulative distribution function method is used;for `p = 1 and q = 1`, beta distribution is reduced to uniform distribution.	Beta
BTPE	Acceptance/rejection method for `ntrial·min(p,1 - p)≥ 30` with decomposition into 4 regions: 2 parallelograms triangle left exponential tail right exponential tail	Binomial
H2PE	Acceptance/rejection method for large mode of distribution with decomposition into 3 regions: rectangular left exponential tail right exponential tail	Hypergeometric
PTPE	Acceptance/rejection method for λ≥ 27 with decomposition into 4 regions: 2 parallelograms triangle left exponential tail right exponential tail; otherwise, table lookup method is used.	Poisson
POISNORM	for λ≥ 1, method based on Poisson inverse CDF approximation by Gaussian inverse CDF; for λ < 1, table lookup method is used.	Poisson, PoissonV
NBAR	Acceptance/rejection method for , 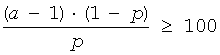with decomposition into 5 regions: rectangular 2 trapezoid left exponential tail right exponential tail	NegBinomial
CHI2GAMMA	Random number generator of chi-square distribution with `ν` degrees of freedom. To generate any successive random number `x` of the chi-square distribution: If `ν` is 1 or 3, a chi-square distributed random number is generated as a sum of squares of `ν` independent normal random numbers with mean value a = 0 and standard deviation `σ` =1. If `ν` is even and 2 ≤ `ν` ≤ 16, a chi-square distributed random number is generated using the formula: where u_i are successive random numbers uniformly distributed over the interval (0, 1) If `ν` ≥ 17 or `ν` is odd and 5 ≤ `ν` ≤ 15, a chi-square distribution is reduced to a Gamma distribution with these parameters: Shape `α` = `ν` / 2 Offset a = 0 Scale factor `β` = 2 The random numbers of the Gamma distribution are generated using the VSL_RNG_METHOD_GAMMA_GNORM method.	ChiSquare

NOTE:

In this document, routines are often referred to by their base name (Gaussian) when this does not lead to ambiguity. In the routine reference, the full name (vsrnggaussian, vsRngGaussian) is always used in prototypes and code examples.

Parent topic: Random Number Generators Conventions

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Random Number Generators Naming Conventions