?tzrzf

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-009DF030-771D-46F4-B9F6-01CBC0746003

View Details

?tzrzf

Reduces the upper trapezoidal matrix A to upper triangular form.

Syntax

call stzrzf(m, n, a, lda, tau, work, lwork, info)

call dtzrzf(m, n, a, lda, tau, work, lwork, info)

call ctzrzf(m, n, a, lda, tau, work, lwork, info)

call ztzrzf(m, n, a, lda, tau, work, lwork, info)

call tzrzf(a [, tau] [,info])

Include Files

mkl.fi, lapack.f90

Description

The routine reduces the m-by-n (m≤n) real/complex upper trapezoidal matrix A to upper triangular form by means of orthogonal/unitary transformations. The upper trapezoidal matrix A = [A1 A2] = [A_{1:m, 1:m}, A_{1:m, m+1:n}] is factored as

A = [R0]*Z,

where Z is an n-by-n orthogonal/unitary matrix, R is an m-by-m upper triangular matrix, and 0 is the m-by-(n-m) zero matrix.

See larz that applies an elementary reflector returned by ?tzrzf to a general matrix.

The ?tzrzf routine replaces the deprecated ?tzrqf routine.

Input Parameters

m

INTEGER. The number of rows in the matrix A (m≥ 0).

n

INTEGER. The number of columns in A (n≥m).

a, work

REAL for stzrzf

DOUBLE PRECISION for dtzrzf

COMPLEX for ctzrzf

DOUBLE COMPLEX for ztzrzf.

Arrays: a(lda,*),work(lwork).

The leading m-by-n upper trapezoidal part of the array a contains the matrix A to be factorized.

The second dimension of a must be at least max(1, n).

work is a workspace array, its dimension max(1, lwork).

lda

INTEGER. The leading dimension of a; at least max(1, m).

lwork

INTEGER. The size of the work array;

lwork≥ max(1, m).

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla.

See Application Notes for the suggested value of lwork.

Output Parameters

a

Overwritten on exit by the factorization data as follows:

the leading m-by-m upper triangular part of a contains the upper triangular matrix R, and elements m +1 to n of the first m rows of a, with the array tau, represent the orthogonal matrix Z as a product of m elementary reflectors.

tau

REAL for stzrzf

DOUBLE PRECISION for dtzrzf

COMPLEX for ctzrzf

DOUBLE COMPLEX for ztzrzf.

Array, size at least max (1, m). Contains scalar factors of the elementary reflectors for the matrix Z.

work(1)

If info = 0, on exit work(1) contains the minimum value of lwork required for optimum performance. Use this lwork for subsequent runs.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine tzrzf interface are the following:

a: Holds the matrix A of size (m,n).
tau: Holds the vector of length (m).

Application Notes

The factorization is obtained by Householder's method. The k-th transformation matrix, Z(k), which is used to introduce zeros into the (m - k + 1)-th row of A, is given in the form

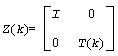
where for real flavors

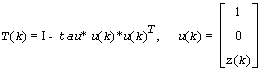
and for complex flavors

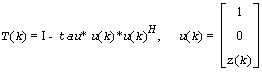
tau is a scalar and z(k) is an l-element vector. tau and z(k) are chosen to annihilate the elements of the k-th row of A2.

The scalar tau is returned in the k-th element of tau and the vector u(k) in the k-th row of A, such that the elements of z(k) are stored in a(k, m+1), ..., a(k, n).

The elements of R are returned in the upper triangular part of A.

The matrix Z is given by

Z = Z(1)*Z(2)*...*Z(m).

For better performance, try using lwork =m*blocksize, where blocksize is a machine-dependent value (typically, 16 to 64) required for optimum performance of the blocked algorithm.

If it is not clear how much workspace to supply, use a generous value of lwork for the first run, or set lwork = -1.

In first case the routine completes the task, though probably not so fast as with a recommended workspace, and provides the recommended workspace in the first element of the corresponding array work on exit. Use this value (work(1)) for subsequent runs.

If lwork = -1, then the routine returns immediately and provides the recommended workspace in the first element of the corresponding array (work). This operation is called a workspace query.

Note that if lwork is less than the minimal required value and is not equal to -1, then the routine returns immediately with an error exit and does not provide any information on the recommended workspace.

Related routines include:

ormrz: to apply matrix Q (for real matrices)
unmrz: to apply matrix Q (for complex matrices).

Parent topic: Orthogonal Factorizations: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?tzrzf

Syntax

Include Files

Description

Input Parameters

Output Parameters

LAPACK 95 Interface Notes

Application Notes