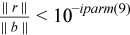pardiso iparm Parameter

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-264E311E-ACED-4D56-AC31-E9D3B11D1CBF

View Details

pardiso iparm Parameter

This table describes all individual components of the Intel® oneAPI Math Kernel Library (oneMKL) PARDISOiparm parameter. Components which are not used must be initialized with 0. Default values are denoted with an asterisk (*).

Component	Description
`iparm(1)` input	Use default values.
	0	`iparm(2)` - `iparm(64)` are filled with default values.
	≠0	You must supply all values in components `iparm(2)` - `iparm(64)`.
`iparm(2)` input	Fill-in reducing ordering for the input matrix. CAUTION: You can control the parallel execution of the solver by explicitly setting the `MKL_NUM_THREADS` environment variable. If fewer OpenMP threads are available than specified, the execution may slow down instead of speeding up. If `MKL_NUM_THREADS` is not defined, then the solver uses all available processors.
	0	The minimum degree algorithm [Li99].
	2*	The nested dissection algorithm from the METIS package [Karypis98].
	3	The parallel (OpenMP) version of the nested dissection algorithm. It can decrease the time of computations on multi-core computers, especially when Intel® oneAPI Math Kernel Library (oneMKL) PARDISO Phase 1 takes significant time. NOTE: Setting `iparm(2)` `= 3` prevents the use of CNR mode (`iparm(34)` `> 0`) because Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses dynamic parallelism.
`iparm(3)`	Reserved. Set to zero.
`iparm(4)` input	Preconditioned CGS/CG. This parameter controls preconditioned CGS [Sonn89] for nonsymmetric or structurally symmetric matrices and Conjugate-Gradients for symmetric matrices. `iparm(4)` has the form `iparm(4)`= `10*L+K`.
	`K`=0	The factorization is always computed as required by phase.
	`K`=1	CGS iteration replaces the computation of `LU`. The preconditioner is `LU` that was computed at a previous step (the first step or last step with a failure) in a sequence of solutions needed for identical sparsity patterns.
	`K`=2	CGS iteration for symmetric positive definite matrices replaces the computation of `LL`^T. The preconditioner is `LL`^T that was computed at a previous step (the first step or last step with a failure) in a sequence of solutions needed for identical sparsity patterns.
	The value `L` controls the stopping criterion of the Krylov Subspace iteration: `eps_CGS = 10^-L` is used in the stopping criterion `\|\|dx_i\|\| / \|\|dx₀\|\| < eps_CGS` where `\|\|dx_i\|\| = \|\|inv(LU)r_i\|\|` for `K = 1` or `\|\|dx_i\|\| = \|\|inv(LL^T)r_i\|\|` for `K = 2` and `r`_i is the residue at iteration `i` of the preconditioned Krylov Subspace iteration. A maximum number of 150 iterations is fixed with the assumption that the iteration will converge before consuming half the factorization time. Intermediate convergence rates and residue excursions are checked and can terminate the iteration process. If `phase =23`, then the factorization for a given `A` is automatically recomputed in cases where the Krylov Subspace iteration failed, and the corresponding direct solution is returned. Otherwise the solution from the preconditioned Krylov Subspace iteration is returned. Using `phase =33` results in an error message (`error=-4`) if the stopping criteria for the Krylov Subspace iteration can not be reached. More information on the failure can be obtained from `iparm(20)`. The default is `iparm(4)=0`, and other values are only recommended for an advanced user. `iparm(4)` must be greater than or equal to zero. Examples: `iparm(4)` Description `31` `LU`-preconditioned CGS iteration with a stopping criterion of 1.0E-3 for nonsymmetric matrices `61` `LU`-preconditioned CGS iteration with a stopping criterion of 1.0E-6 for nonsymmetric matrices `62` `LL`^T-preconditioned CGS iteration with a stopping criterion of 1.0E-6 for symmetric positive definite matrices
`iparm(5)` input	User permutation. This parameter controls whether user supplied fill-in reducing permutation is used instead of the integrated multiple-minimum degree or nested dissection algorithms. Another use of this parameter is to control obtaining the fill-in reducing permutation vector calculated during the reordering stage of Intel® oneAPI Math Kernel Library (oneMKL) PARDISO. This option is useful for testing reordering algorithms, adapting the code to special applications problems (for instance, to move zero diagonal elements to the end of `PAP^T`), or for using the permutation vector more than once for matrices with identical sparsity structures. For definition of the permutation, see the description of the perm parameter. CAUTION: You can only set one of `iparm(5)`, `iparm(31)`, and `iparm(36)`, so be sure that the `iparm(31)` (partial solution) and the `iparm(36)` (Schur complement) parameters are 0 if you set `iparm(5)`.
	0*	User permutation in the perm array is ignored.
	1	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses the user supplied fill-in reducing permutation from theperm array. `iparm(2)` is ignored. NOTE: Setting `iparm(5)` = 1 prevents use of a parallel algorithm for the solve step.
	2	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO returns the permutation vector computed at phase 1 in theperm array.
`iparm(6)` input	Write solution on x. NOTE: The array x is always used.
	0*	The array x contains the solution; right-hand side vector b is kept unchanged.
	1	The solver stores the solution on the right-hand side b.
`iparm(7)` output	Number of iterative refinement steps performed. Reports the number of iterative refinement steps that were actually performed during the solve step.
`iparm(8)` input	Iterative refinement step. On entry to the solve and iterative refinement step, `iparm(8)` must be set to the maximum number of iterative refinement steps that the solver performs. NOTE: Perturbed pivots result in iterative refinement (independent of the value of `iparm(8)`) and the number of executed iterations is reported in `iparm(7)`.
	0*	The solver automatically performs two steps of iterative refinement when perturbed pivots are obtained during the numerical factorization.
	>0	Maximum number of iterative refinement steps that the solver performs. The solver performs not more than the absolute value of `iparm(8)` steps of iterative refinement. The solver might stop the process before the maximum number of steps if a satisfactory level of accuracy of the solution in terms of backward error is achieved, or if it determines that the required accuracy cannot be reached. In this case the solver returns -4 in the error parameter. The number of executed iterations is reported in `iparm(7)`.
	<0	Maximum number of iterative refinement steps with a negative sign. Unlike the case above the accumulation of the residuum uses extended precision real and complex data types. NOTE: Currently, this feature is only supported for sequential and OpenMP threading.
`iparm(9)` input	Tolerance level for the relative residual in the iterative refinement process. If set to a non-zero value, an additional criterion is used for stopping the iterative refinement: If set to zero, default checks are used to determine when to stop the iterations (see `iparm(8)` description). NOTE: Currently it is only used for `iparm(24)`=1 or 10 and OpenMP threading.
`iparm(10)` input	Pivoting perturbation. This parameter instructs Intel® oneAPI Math Kernel Library (oneMKL) PARDISO how to handle small pivots or zero pivots for nonsymmetric matrices (`mtype =11` or `mtype =13`) and symmetric matrices (`mtype =-2`, `mtype =-4`, or `mtype =6`). For these matrices the solver uses a complete supernode pivoting approach. When the factorization algorithm reaches a point where it cannot factor the supernodes with this pivoting strategy, it uses a pivoting perturbation strategy similar to [Li99], [Schenk04]. Small pivots are perturbed with `eps = 10^-iparm(10)`. The magnitude of the potential pivot is tested against a constant threshold of `alpha = eps\|\|A2\|\|_inf,` where `eps = 10^(-iparm(10))`, `A2 = PP_MPSD_rAD_cP`, and `\|\|A2\|\|_inf` is the infinity norm of the scaled and permuted matrix `A`. Any tiny pivots encountered during elimination are set to the sign `(l_II)eps\|\|A2\|\|_inf`, which trades off some numerical stability for the ability to keep pivots from getting too small. Small pivots are therefore perturbed with `eps = 10^(-iparm(10))`.
	13*	The default value for nonsymmetric matrices(mtype =11, mtype=13), `eps = 10^-13`.
	8*	The default value for symmetric indefinite matrices (mtype =-2, mtype=-4, mtype=6), `eps = 10^-8`.
`iparm(11)` input	Scaling vectors. Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses a maximum weight matching algorithm to permute large elements on the diagonal and to scale so that the diagonal elements are equal to 1 and the absolute values of the off-diagonal entries are less than or equal to 1. This scaling method is applied only to nonsymmetric matrices (mtype = 11 or mtype = 13). The scaling can also be used for symmetric indefinite matrices (mtype = -2, mtype =-4, or mtype = 6) when the symmetric weighted matchings are applied (`iparm(13)` = 1). Use `iparm(11)` = 1 (scaling) and `iparm(13)` = 1 (matching) for highly indefinite symmetric matrices, for example, from interior point optimizations or saddle point problems. Note that in the analysis phase (phase=11) you must provide the numerical values of the matrix `A` in array a in case of scaling and symmetric weighted matching.
	0*	Disable scaling. Default for symmetric indefinite matrices.
	1*	Enable scaling. Default for nonsymmetric matrices. Scale the matrix so that the diagonal elements are equal to 1 and the absolute values of the off-diagonal entries are less or equal to 1. This scaling method is applied to nonsymmetric matrices (mtype = 11, mtype = 13). The scaling can also be used for symmetric indefinite matrices (mtype = -2, mtype = -4, mtype = 6) when the symmetric weighted matchings are applied (`iparm(13)` = 1). Note that in the analysis phase (phase=11) you must provide the numerical values of the matrix `A` in case of scaling.
`iparm(12)` input	Solve with transposed or conjugate transposed matrix `A`. NOTE: For real matrices, the terms transposed and conjugate transposed are equivalent.
	0*	Solve a linear system `AX` = `B`.
	1	Solve a conjugate transposed system `A`^H`X` = `B` based on the factorization of the matrix `A`.
	2	Solve a transposed system `A`^T`X` = `B` based on the factorization of the matrix `A`.
`iparm(13)` input	Improved accuracy using (non-) symmetric weighted matching. Intel® oneAPI Math Kernel Library (oneMKL) PARDISO can use a maximum weighted matching algorithm to permute large elements close the diagonal. This strategy adds an additional level of reliability to the factorization methods and complements the alternative of using more complete pivoting techniques during the numerical factorization.
	0*	Disable matching. Default for symmetric indefinite matrices.
	1*	Enable matching. Default for nonsymmetric matrices. Maximum weighted matching algorithm to permute large elements close to the diagonal. It is recommended to use `iparm(11)` = 1 (scaling) and `iparm(13)`= 1 (matching) for highly indefinite symmetric matrices, for example from interior point optimizations or saddle point problems. Note that in the analysis phase (phase=11) you must provide the numerical values of the matrix `A` in case of symmetric weighted matching.
`iparm(14)` output	Number of perturbed pivots. After factorization, contains the number of perturbed pivots for the matrix types: 1, 3, 11, 13, -2, -4 and 6.
`iparm(15)` output	Peak memory on symbolic factorization. The total peak memory in kilobytes that the solver needs during the analysis and symbolic factorization phase. This value is only computed in phase 1.
`iparm(16)` output	Permanent memory on symbolic factorization. Permanent memory from the analysis and symbolic factorization phase in kilobytes that the solver needs in the factorization and solve phases. This value is only computed in phase 1.
`iparm(17)` output	Size of factors/Peak memory on numerical factorization and solution. This parameter provides the size in kilobytes of the total memory consumed by in-core Intel® oneAPI Math Kernel Library (oneMKL) PARDISO for internal floating point arrays. This parameter is computed in phase 1. See`iparm(63)` for the OOC mode. The total peak memory consumed by Intel® oneAPI Math Kernel Library (oneMKL) PARDISO is`max(iparm(15), iparm(16)+iparm(17))`
`iparm(18)` input/output	Report the number of non-zero elements in the factors.
	<0	Enable reporting if `iparm(18)` < 0 on entry. The default value is -1.
	>=0	Disable reporting.
`iparm(19)` input/output	Report number of floating point operations (in 10⁶ floating point operations) that are necessary to factor the matrix `A`.
	<0	Enable report if `iparm(19)` < 0 on entry. This increases the reordering time.
	>=0 *	Disable report.
`iparm(20)` output	Report CG/CGS diagnostics.
	>0	CGS succeeded, reports the number of completed iterations.
	<0	CG/CGS failed (error=-4 after the solution phase). If `phase= 23`, then the factors `L` and `U` are recomputed for the matrix `A` and the error flag `error=0` in case of a successful factorization. If `phase = 33`, then `error = -4` signals failure. `iparm(20)= - it_cgs*10 - cgs_error`. Possible values of `cgs_error`: 1 - fluctuations of the residuum are too large 2 - `\|\|dx_{max_it_cgs/2}\|\|` is too large (slow convergence) 3 - stopping criterion is not reached at `max_it_cgs` 4 - perturbed pivots caused iterative refinement 5 - factorization is too fast for this matrix. It is better to use the factorization method with `iparm(4)` = 0
`iparm(21)` input	Pivoting for symmetric indefinite matrices. NOTE: Use `iparm(11)` = 1 (scaling) and `iparm(13)` = 1 (matchings) for highly indefinite symmetric matrices, for example from interior point optimizations or saddle point problems.
	0	Apply 1x1 diagonal pivoting during the factorization process.
	1*	Apply 1x1 and 2x2 Bunch-Kaufman pivoting during the factorization process. Bunch-Kaufman pivoting is available for matrices of `mtype=-2`, `mtype=-4`, or `mtype=6`.
	2	Apply 1x1 diagonal pivoting during the factorization process. Using this value is the same as using `iparm(21)` = 0 except that the solve step does not automatically make iterative refinements when perturbed pivots are obtained during numerical factorization. The number of iterations is limited to the number of iterative refinements specified by `iparm(8)` (0 by default).
	3	Apply 1x1 and 2x2 Bunch-Kaufman pivoting during the factorization process. Bunch-Kaufman pivoting is available for matrices of `mtype=-2`, `mtype=-4`, or `mtype=6`. Using this value is the same as using `iparm(21)` = 1 except that the solve step does not automatically make iterative refinements when perturbed pivots are obtained during numerical factorization. The number of iterations is limited to the number of iterative refinements specified by `iparm(8)` (0 by default).
`iparm(22)` output	Inertia: number of positive eigenvalues. Intel® oneAPI Math Kernel Library (oneMKL) PARDISO reports the number of positive eigenvalues for symmetric indefinite matrices.
`iparm(23)` output	Inertia: number of negative eigenvalues. Intel® oneAPI Math Kernel Library (oneMKL) PARDISO reports the number of negative eigenvalues for symmetric indefinite matrices.
`iparm(24)` input	Parallel factorization control.
	0*	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses the classic algorithm for factorization.
	1	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses a two-level factorization algorithm. This algorithm generally improves scalability in case of parallel factorization on many OpenMP threads (more than eight). NOTE: Disable `iparm(11)` (scaling) and `iparm(13)`= 1 (matching) when using the two-level factorization algorithm. Otherwise Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses the classic factorization algorithm.
	10	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses an improved two-level factorization algorithm for nonsymmetric matrices.
`iparm(25)` input	Parallel forward/backward solve control.
	0*	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses the following strategy for parallelizing the solving step: In the case of the one right-hand side, the parallelization will be performed by partitioning the matrix. Otherwise, the parallelization will be over the right-hand sides. This feature is available only for in-core Intel® oneAPI Math Kernel Library (oneMKL) PARDISO (see`iparm(60)`).
	1	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses the sequential forward and backward solve.
	2	Independent from the number of the right-hand sides, Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses the parallel algorithm based on the matrix partitioning. This feature is available only for in-core Intel® oneAPI Math Kernel Library (oneMKL) PARDISO (see`iparm(60)`).
`iparm(26)`	Reserved. Set to zero.
`iparm(27)` input	Matrix checker.
	0*	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO does not check the sparse matrix representation for errors.
	1	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO checks integer arraysia and ja. In particular, Intel® oneAPI Math Kernel Library (oneMKL) PARDISO checks whether column indices are sorted in increasing order within each row.
`iparm(28)` input	Single or double precision Intel® oneAPI Math Kernel Library (oneMKL) PARDISO. See `iparm(8)` for information on controlling the precision of the refinement steps. IMPORTANT: The `iparm(28)`value is stored in the Intel® oneAPI Math Kernel Library (oneMKL) PARDISO handle between Intel® oneAPI Math Kernel Library (oneMKL) PARDISO calls, so the precision mode can be changed only during phase 1.
	0*	Input arrays (a, x and b) and all internal arrays must be presented in double precision.
	1	Input arrays (a, x and b) must be presented in single precision. In this case all internal computations are performed in single precision.
`iparm(29)`	Reserved. Set to zero.
`iparm(30)` output	Number of zero or negative pivots. If Intel® oneAPI Math Kernel Library (oneMKL) PARDISO detects zero or negative pivot formtype=2 or mtype=4 matrix types, the factorization is stopped. Intel® oneAPI Math Kernel Library (oneMKL) PARDISO returns immediately with anerror = -4, and `iparm(30)` reports the number of the equation where the zero or negative pivot is detected. Note: The returned value can be different for the parallel and sequential version in case of several zero/negative pivots.
`iparm(31)` input	Partial solve and computing selected components of the solution vectors. This parameter controls the solve step of Intel® oneAPI Math Kernel Library (oneMKL) PARDISO. It can be used if only a few components of the solution vectors are needed or if you want to reduce the computation cost at the solve step by utilizing the sparsity of the right-hand sides. To use this option the input permutation vector defineperm so that when perm`(i)` = 1 it means that either the `i`-th component in the right-hand sides is nonzero, or the `i`-th component in the solution vectors is computed, or both, depending on the value of `iparm(31)`. The permutation vector permmust be present in all phases of Intel® oneAPI Math Kernel Library (oneMKL) PARDISO software. At the reordering step, the software overwrites the input vectorperm by a permutation vector used by the software at the factorization and solver step. If m is the number of components such that perm`(i)` = 1, then the last m components of the output vector perm are a set of the indices `i` satisfying the condition perm`(i)` = 1 on input. NOTE: Turning on this option often increases the time used by Intel® oneAPI Math Kernel Library (oneMKL) PARDISO for factorization and reordering steps, but it can reduce the time required for the solver step. IMPORTANT: You can use this feature for both in-core and out-of-core Intel® oneAPI Math Kernel Library (oneMKL) PARDISO as long as iparm[23]=1. Otherwise, you cannot use partial solve for out-of-core mode and you will need to set`iparm(60)`=0 for in-core mode. Set the parameters `iparm(8)` (iterative refinement steps), `iparm(4)` (preconditioned CGS), `iparm(5)` (user permutation), and `iparm(36)` (Schur complement) to 0 as well.
	0*	Disables this option.
	1	it is assumed that the right-hand sides have only a few non-zero components^* and the input permutation vector perm is defined so that perm`(i)` = 1 means that the (`i`)-th component in the right-hand sides is nonzero. In this case Intel® oneAPI Math Kernel Library (oneMKL) PARDISO only uses the non-zero components of the right-hand side vectors and computes only corresponding components in the solution vectors. That means the`i`-th component in the solution vectors is only computed if perm`(i)` = 1.
	2	It is assumed that the right-hand sides have only a few non-zero components^* and the input permutation vector perm is defined so that perm`(i)` = 1 means that the `i`-th component in the right-hand sides is nonzero. Unlike for `iparm(31)`=1, all components of the solution vector are computed for this setting and all components of the right-hand sides are used. Because all components are used, for `iparm(31)`=2 you must set the `i`-th component of the right-hand sides to zero explicitly if perm`(i)` is not equal to 1.
	3	Selected components of the solution vectors are computed. The perm array is not related to the right-hand sides and it only indicates which components of the solution vectors should be computed. In this case perm`(i)` = 1 means that the `i`-th component in the solution vectors is computed.
`iparm(32)` - `iparm(33)`	Reserved. Set to zero.
`iparm(34)` input	Optimal number of OpenMP threads for conditional numerical reproducibility (CNR) mode. Intel® oneAPI Math Kernel Library (oneMKL) PARDISO reads the value of`iparm(34)` during the analysis phase (phase 1), so you cannot change it later. Because Intel® oneAPI Math Kernel Library (oneMKL) PARDISO uses C random number generator facilities during the analysis phase (phase 1) you must take these precautions to get numerically reproducible results: Do not alter the states of the random number generators. Do not run multiple instances of Intel® oneAPI Math Kernel Library (oneMKL) PARDISO in parallel in the analysis phase (phase 1). NOTE: CNR is only available for the in-core version of Intel® oneAPI Math Kernel Library (oneMKL) PARDISO and the non-parallel version of the nested dissection algorithm. You must also: set `iparm(60)` to 0 in order to use the in-core version, not set `iparm(2)` to 3 in order to not use the parallel version of the nested dissection algorithm. Otherwise Intel® oneAPI Math Kernel Library (oneMKL) PARDISO does not produce numerically repeatable results even if CNR is enabled for Intel® oneAPI Math Kernel Library (oneMKL) using the functionality described inSupport Functions for CNR.
	0*	CNR mode for Intel® oneAPI Math Kernel Library (oneMKL) PARDISO is enabled only if it is enabled for Intel® oneAPI Math Kernel Library (oneMKL) using the functionality described inSupport Functions for CNRand the in-core version is used. Intel® oneAPI Math Kernel Library (oneMKL) PARDISO determines the optimal number of OpenMP threads automatically, and produces numerically reproducible results regardless of the number of threads.
	>0	CNR mode is enabled for Intel® oneAPI Math Kernel Library (oneMKL) PARDISO if in-core version is used and the optimal number of OpenMP threads for Intel® oneAPI Math Kernel Library (oneMKL) PARDISO to rely on is defined by the value of`iparm(34)`. You can use `iparm(34)`to enable CNR mode independent from other Intel® oneAPI Math Kernel Library (oneMKL) domains. To get the best performance, set`iparm(34)`to the actual number of hardware threads dedicated for Intel® oneAPI Math Kernel Library (oneMKL) PARDISO. Setting`iparm(34)` to fewer OpenMP threads than the maximum number of them in use reduces the scalability of the problem being solved. Setting `iparm(34)`to more threads than are available can reduce the performance of Intel® oneAPI Math Kernel Library (oneMKL) PARDISO.
`iparm(35)` input	One- or zero-based indexing of columns and rows. NOTE: Schur complement may be inaccurate or incorrect if pivots are detected. Please, check the output of `iparm(29)` .
	0*	One-based indexing: columns and rows indexing in arrays ia, ja, and perm starts from 1 (Fortran-style indexing).
	1	Zero-based indexing: columns and rows indexing in arrays ia, ja, and perm starts from 0 (C-style indexing).
`iparm(36)` input/output	Schur complement matrix computation control. To calculate this matrix, you must set the input permutation vector perm to a set of indexes such that when `perm(i) = 1`, the `i`-th element of the initial matrix is an element of the Schur matrix. CAUTION: You can only set one of `iparm(5)`, `iparm(31)`, and `iparm(36)`, so be sure that the `iparm(5)` (user permutation) and the `iparm(31)` (partial solution) parameters are 0 if you set `iparm(36)`.
	0*	Do not compute Schur complement.
	1	Compute Schur complement matrix as part of Intel® oneAPI Math Kernel Library (oneMKL) PARDISO factorization step and return it in the solution vector. NOTE: This option only computes the Schur complement matrix, and does not calculate factorization arrays.
	2	Compute Schur complement matrix as part of Intel® oneAPI Math Kernel Library (oneMKL) PARDISO factorization step and return it in the solution vector. Since this option calculates factorization arrays you can use it to launch partial or full solution of the entire problem after the factorization step.
	-1	Same as `iparm(36)` equals 1, but the Schur complement matrix is provided in 3-array CSR sparse format. Use in combination with pardiso_export. After reordering stage of MKL PARDISO, `iparm(36)` contains number of nonzero elements for Schur complement matrix. Set it once again before calling the factorization phase. NOTE: This option is available only when `iparm(24)`is not equal to 0.
	-2	Same as `iparm(36)` equals 2, but the Schur complement matrix is provided in 3-array CSR sparse format. Use in combination with pardiso_export. After reordering stage of MKL PARDISO, `iparm(36)` contains number of nonzero elements for Schur complement matrix. Set it once again before calling the factorization phase. NOTE: This option is available only when `iparm(24)`is not equal to 0.
`iparm(37)` input	Format for matrix storage.
	0*	Use CSR format (see Three Array Variation of CSR Format) for matrix storage.
	> 0	Use BSR format (see Three Array Variation of BSR Format) for matrix storage with blocks of size `iparm(37)`. NOTE: Intel® oneAPI Math Kernel Library (oneMKL) does not support BSR format in these cases: `iparm(11)` `> 0`: Scaling vectors `iparm(13)` `> 0`: Weighted matching `iparm(31)` `> 0`: Partial solution `iparm(36)` `> 0`: Schur complement `iparm(56)` `> 0`: Pivoting control `iparm(60)` `> 0`: OOC Intel® oneAPI Math Kernel Library (oneMKL) PARDISO
	< 0	Convert supplied matrix to variable BSR (VBSR) format (see Sparse Data Storage) for matrix storage. Intel® oneAPI Math Kernel Library (oneMKL) PARDISO analyzes the matrix provided in CSR3 format and converts it to an internal VBSR format. Set`iparm(37)` `= -t`, 0 < `t`≤ 100. NOTE: Intel® oneAPI Math Kernel Library (oneMKL) supports only the VBSR format for real and symmetric positive definite or indefinite matrices (mtype = 2 or mtype= -2). Intel® oneAPI Math Kernel Library (oneMKL) does not support VBSR format in these cases: `iparm(11)` `> 0`: Scaling vectors `iparm(13)` `> 0`: Weighted matching `iparm(56)` `> 0`: Pivoting control NOTE: Intel® oneAPI Math Kernel Library (oneMKL) supports these features for all matrix types as long as`iparm(24)`=1: `iparm(31)` `> 0`: Partial solution `iparm(36)` `> 0`: Schur complement `iparm(60)` `> 0`: OOC Intel® oneAPI Math Kernel Library (oneMKL) PARDISO
`iparm(38)`	Reserved. Set to zero.
`iparm(39)`	Enable low rank update (see Low Rank Update) to accelerate factorization for multiple matrices with identical structure and similar values.
	0*	Do not use low rank update functionality.
	1	Use low rank update functionality. You must also set `iparm(24) = 10` and provide a list of changed values in the perm array. This option requires the default settings of `iparm(4)`, `iparm(5)`, `iparm(6)`, `iparm(12)`, `iparm(28)`, `iparm(31)`, `iparm(36)`, `iparm(37)`, `iparm(56)`, and `iparm(60)` as well.
`iparm(40)` - `iparm(42)`	Reserved. Set to zero.
`iparm(43)`	Control parameter for the computation of the diagonal of inverse matrix.
	0*	Do not compute the diagonal of inverse matrix.
	1	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO computes the diagonal of the inverse matrix during the factorization phase. This feature is only available with two-level factorization algorithm (`iparm(24)` = 1) and real symmetric matrices (mtype = 2 or mtype = -2). The diagonal is returned in the solution vector.
`iparm(44)` - `iparm(55)`	Reserved. Set to zero.
`iparm(56)`	Diagonal and pivoting control.
	0*	Internal function used to work with pivot and calculation of diagonal arrays turned off.
	1	You can use the mkl_pardiso_pivot callback routine to control pivot elements which appear during numerical factorization. Additionally, you can obtain the elements of initial matrix and factorized matrices after the pardiso factorization step diagonal using the pardiso_getdiagroutine. This parameter can be turned on only in the in-core version of Intel® oneAPI Math Kernel Library (oneMKL) PARDISO.
`iparm(57)` - `iparm(59)`	Reserved. Set to zero.
`iparm(60)` input	Intel® oneAPI Math Kernel Library (oneMKL) PARDISO mode. `iparm(60)`switches between in-core (IC) and out-of-core (OOC) Intel® oneAPI Math Kernel Library (oneMKL) PARDISO. OOC can solve very large problems by holding the matrix factors in files on the disk, which requires a reduced amount of main memory compared to IC. Unless you are operating in sequential mode, you can switch between IC and OOC modes after the reordering phase. However, you can get better Intel® oneAPI Math Kernel Library (oneMKL) PARDISO performance by setting`iparm(60)` before the reordering phase. The amount of memory used in OOC mode depends on the number of OpenMP threads. WARNING: Do not increase the number of OpenMP threads used for cluster_sparse_solver between the first call and the factorization or solution phase. Because the minimum amount of memory required for out-of-core execution depends on the number of OpenMP threads, increasing it after the initial call can cause incorrect results.
	0*	IC mode.
	1	IC mode is used if the total amount of RAM (in megabytes) needed for storing the matrix factors is less than sum of two values of the environment variables: MKL_PARDISO_OOC_MAX_CORE_SIZE (default value 2000 MB) and MKL_PARDISO_OOC_MAX_SWAP_SIZE (default value 0 MB); otherwise OOC mode is used. In this case amount of RAM used by OOC mode cannot exceed the value of MKL_PARDISO_OOC_MAX_CORE_SIZE. If the total peak memory needed for storing the local arrays is more than MKL_PARDISO_OOC_MAX_CORE_SIZE, increase MKL_PARDISO_OOC_MAX_CORE_SIZE if possible. NOTE: Conditional numerical reproducibility (CNR) is not supported for this mode.
	2	OOC mode. The OOC mode can solve very large problems by holding the matrix factors in files on the disk. Hence the amount of RAM required by OOC mode is significantly reduced compared to IC mode. If the total peak memory needed for storing the local arrays is more than MKL_PARDISO_OOC_MAX_CORE_SIZE, increase MKL_PARDISO_OOC_MAX_CORE_SIZE if possible. To obtain better Intel® oneAPI Math Kernel Library (oneMKL) PARDISO performance, during the numerical factorization phase you can provide the maximum number of right-hand sides, which can be used further during the solving phase. Refer to How to use Intel® MKL OOC PARDISO and Storage of Matrices for more details about OOC.
`iparm(61)` - `iparm(62)`	Reserved. Set to zero.
`iparm(63)` output	Size of the minimum OOC memory for numerical factorization and solution. This parameter provides the size in kilobytes of the minimum memory required by OOC Intel® oneAPI Math Kernel Library (oneMKL) PARDISO for internal floating point arrays. This parameter is computed in phase 1. Total peak memory consumption of OOC Intel® oneAPI Math Kernel Library (oneMKL) PARDISO can be estimated asmax(`iparm(15)`, `iparm(16)` + `iparm(63)`).
`iparm(64)`	Reserved. Set to zero.

NOTE:

Generally in sparse matrices, components which are equal to zero can be considered non-zero if necessary. For example, in order to make a matrix structurally symmetric, elements which are zero can be considered non-zero. See Sparse Matrix Storage Formats for an example.

Product and Performance Information
Performance varies by use, configuration and other factors. Learn more at www.Intel.com/PerformanceIndex. Notice revision #20201201

Product and Performance Information

Performance varies by use, configuration and other factors. Learn more at www.Intel.com/PerformanceIndex.

Notice revision #20201201

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

pardiso iparm Parameter