?unghr

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-3D274DD7-1977-4DB7-B39F-DCEC320D3435

View Details

?unghr

Generates the complex unitary matrix Q determined by ?gehrd.

Syntax

lapack_int LAPACKE_cunghr (int matrix_layout, lapack_int n, lapack_int ilo, lapack_int ihi, lapack_complex_float* a, lapack_int lda, const lapack_complex_float* tau);

lapack_int LAPACKE_zunghr (int matrix_layout, lapack_int n, lapack_int ilo, lapack_int ihi, lapack_complex_double* a, lapack_int lda, const lapack_complex_double* tau);

Include Files

mkl.h

Description

The routine is intended to be used following a call to cgehrd/zgehrd, which reduces a complex matrix A to upper Hessenberg form H by a unitary similarity transformation: A = Q*H*Q^H. ?gehrd represents the matrix Q as a product of ihi-iloelementary reflectors. Here ilo and ihi are values determined by cgebal/zgebal when balancing the matrix; if the matrix has not been balanced, ilo = 1 and ihi = n.

Use the routine unghr to generate Q explicitly as a square matrix. The matrix Q has the structure:

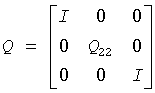
where Q₂₂ occupies rows and columns ilo to ihi.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

n

The order of the matrix Q (n≥ 0).

ilo, ihi

These must be the same parameters ilo and ihi, respectively, as supplied to ?gehrd . (If n > 0, then 1 ≤ilo≤ihi≤n. If n = 0, then ilo = 1 and ihi = 0.)

a, tau

Arrays:

a (size max(1, lda*n)) contains details of the vectors which define the elementary reflectors, as returned by ?gehrd.

tau contains further details of the elementary reflectors, as returned by ?gehrd .

The dimension of tau must be at least max (1, n-1).

lda

The leading dimension of a; at least max(1, n).

Output Parameters

a: Overwritten by the n-by-n unitary matrix Q.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Application Notes

The computed matrix Q differs from the exact result by a matrix E such that ||E||₂ = O(ε), where ε is the machine precision.

The approximate number of real floating-point operations is (16/3)(ihi-ilo)³.

The real counterpart of this routine is orghr.

Parent topic: Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?unghr