Summary Statistics Mathematical Notation and Definitions

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-BDDBC072-5286-407F-B5CC-3EA4F146EF77

View Details

Summary Statistics Mathematical Notation and Definitions

The following notations are used in the mathematical definitions and the description of the Intel® oneAPI Math Kernel Library Summary Statistics functions.

Matrix and Weights of Observations

For a random p-dimensional vector ξ = (ξ₁,..., ξ_i,..., ξ_p), this manual denotes the following:

(X)_i=(x_ij)_j=1..n is the result of n independent observations for the i-th component ξ_i of the vector ξ.
The two-dimensional array X=(x_ij)_{n x p} is the matrix of observations.
The column [X]_j=(x_ij)_i=1..p of the matrix X is the j-th observation of the random vector ξ.

Each observation [X]_j is assigned a non-negative weight w_j , where

The vector (w_j)_j=1..n is a vector of weights corresponding to n observations of the random vector ξ.
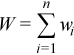
is the accumulated weight corresponding to observations X.

Vector of sample means

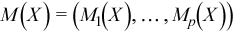with

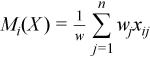
for all i = 1, ..., p.

Vector of sample partial sums

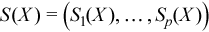with

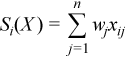
for all i = 1, ..., p.

Vector of sample variances

with ,

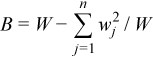
for all i = 1, ..., p.

Vector of sample raw/algebraic moments of `k`-th order, `k`≥ 1

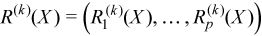with

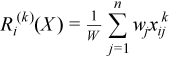
for all i = 1, ..., p.

Vector of sample raw/algebraic partial sums of `k`-th order, `k`= 2, 3, 4 (raw/algebraic partial sums of squares/cubes/fourth powers)

with

for all i = 1, ..., p.

Vector of sample central moments of the third and the fourth order

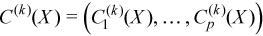with ,

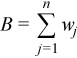
for all i = 1, ..., p and k = 3, 4.

Vector of sample central partial sums of `k`-th order, `k`= 2, 3, 4 (central partial sums of squares/cubes/fourth powers)

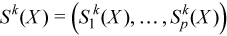with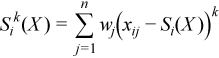

for all i = 1, ..., p.

Vector of sample excess kurtosis values

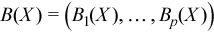with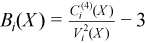

for all i = 1, ..., p.

Vector of sample skewness values

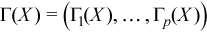with

for all i = 1, ..., p.

Vector of sample variation coefficients

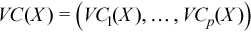with

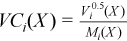
for all i = 1, ..., p.

Matrix of order statistics

Matrix Y = (y_ij)_pxn, in which the i-th row (Y)_i = (y_ij)_j=1..n is obtained as a result of sorting in the ascending order of row (X)_i = (x_ij)_j=1..n in the original matrix of observations.

Vector of sample minimum values

, where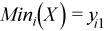

for all i = 1, ..., p.

Vector of sample maximum values

, where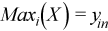

for all i = 1, ..., p.

Vector of sample median values

, where

for all i = 1, ..., p.

Vector of sample median absolute deviations

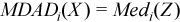, where with ,

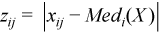
for all i = 1, ..., p.

Vector of sample mean absolute deviations

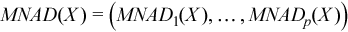, where 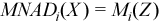with ,

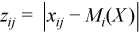
for all i = 1, ..., p.

Vector of sample quantile values

For a positive integer number q and k belonging to the interval [0, q-1], point z_i is the k-th q quantile of the random variable ξ_i if P{ξ_i≤z_i} ≥β and P{ξ_i≤z_i} ≥ 1 - β, where

P is the probability measure.
β = k/n is the quantile order.

The calculation of quantiles is as follows:

j = [(n-1)β] and f = {(n-1)β} as integer and fractional parts of the number (n-1)β, respectively, and the vector of sample quantile values is

Q(X,β) = (Q₁(X,β), ..., Q_p(X,β))

where

(Q_i(X,β) = y_i,j+1 + f(y_i,j+2 - y_i,j+1)

for all i = 1, ..., p.

Variance-covariance matrix

C(X) = (c_ij(X))_{p x p}

where

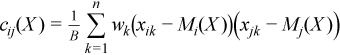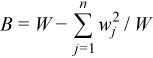
Cross-product matrix (matrix of cross-products and sums of squares)

CP(X) = (cp_ij(X))_{p x p}

where

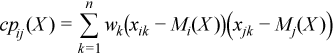
Pooled and group variance-covariance matrices

The set N = {1, ..., n} is partitioned into non-intersecting subsets

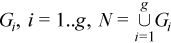
The observation [X]_j = (x_ij)_i=1..p belongs to the group r if j∈G_r. One observation belongs to one group only. The group mean and variance-covariance matrices are calculated similarly to the formulas above:

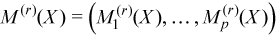with ,

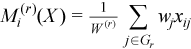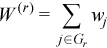
for all i = 1, ..., p,

where

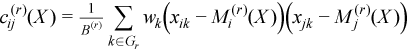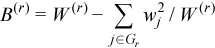
for all i = 1, ..., p and j = 1, ..., p.

A pooled variance-covariance matrix and a pooled mean are computed as weighted mean over group covariance matrices and group means, correspondingly:

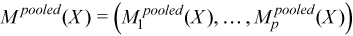with

for all i = 1, ..., p,

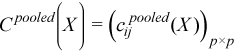for all i = 1, ..., p and j = 1, ..., p.

Correlation matrix

, where

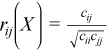
for all i = 1, ..., p and j = 1, ..., p.

Partial variance-covariance matrix

For a random vector ξ partitioned into two components Z and Y, a variance-covariance matrix C describes the structure of dependencies in the vector ξ:

The partial covariance matrix P(X) =(p_ij(X))_kxk is defined as

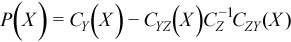where k is the dimension of Y.

Partial correlation matrix

The following is a partial correlation matrix for all i = 1, ..., k and j = 1, ..., k:

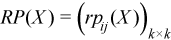, where

where

k is the dimension of Y.
p_ij(X) are elements of the partial variance-covariance matrix.

Sorted dataset

Matrix Y = (y_ij)_pxn, in which the i-th row (Y)_i is obtained as a result of sorting in ascending order the row (X)_i = (x_ij)_{j = 1..n} in the original matrix of observations.

Parent topic: Summary Statistics

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C