p?larft

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-B2F36D3E-02BB-4364-B30B-FA862B96C7B0

View Details

p?larft

Forms the triangular vector T of a block reflector H=I-V*T*V^H.

Syntax

void pslarft (char *direct , char *storev , MKL_INT *n , MKL_INT *k , float *v , MKL_INT *iv , MKL_INT *jv , MKL_INT *descv , float *tau , float *t , float *work );

void pdlarft (char *direct , char *storev , MKL_INT *n , MKL_INT *k , double *v , MKL_INT *iv , MKL_INT *jv , MKL_INT *descv , double *tau , double *t , double *work );

void pclarft (char *direct , char *storev , MKL_INT *n , MKL_INT *k , MKL_Complex8 *v , MKL_INT *iv , MKL_INT *jv , MKL_INT *descv , MKL_Complex8 *tau , MKL_Complex8 *t , MKL_Complex8 *work );

void pzlarft (char *direct , char *storev , MKL_INT *n , MKL_INT *k , MKL_Complex16 *v , MKL_INT *iv , MKL_INT *jv , MKL_INT *descv , MKL_Complex16 *tau , MKL_Complex16 *t , MKL_Complex16 *work );

Include Files

mkl_scalapack.h

Description

The p?larftfunction forms the triangular factor T of a real/complex block reflector H of order n, which is defined as a product of k elementary reflectors.

If direct = 'F', H = H(1)*H(2)...*H(k), and T is upper triangular;

If direct = 'B', H = H(k)*...*H(2)*H(1), and T is lower triangular.

If storev = 'C', the vector which defines the elementary reflector H(i) is stored in the i-th column of the distributed matrix V, and

H = I-V*T*V'

If storev = 'R', the vector which defines the elementary reflector H(i) is stored in the i-th row of the distributed matrix V, and

H = I-V'*T*V.

Input Parameters

direct

(global)

Specifies the order in which the elementary reflectors are multiplied to form the block reflector:

if direct = 'F': H = H(1)*H(2)*...*H(k) (forward)

if direct = 'B': H = H(k)*...*H(2)*H(1) (backward).

storev

(global)

Specifies how the vectors that define the elementary reflectors are stored (See Application Notes below):

if storev = 'C': columnwise;

if storev = 'R': rowwise.

n

(global)

The order of the block reflector H. n ≥ 0.

k

(global)

The order of the triangular factor T, is equal to the number of elementary reflectors.

1 ≤ k ≤ mb_v (= nb_v).

v

Pointer into the local memory to an array of local size

LOCr(iv+n-1) * LOCc(jv+k-1) if storev = 'C', and

LOCr(iv+k-1) * LOCc(jv+n-1) if storev = 'R'.

The distributed matrix V contains the Householder vectors. (See Application Notes below).

iv, jv

(global)

The row and column indices in the global matrix V indicating the first row and the first column of the matrix sub(V), respectively.

descv

(local) array of size dlen_. The array descriptor for the distributed matrix V.

tau

(local)

Array of size LOCr(iv+k-1) if incv = m_v, and LOCc(jv+k-1) otherwise. This array contains the Householder scalars related to the Householder vectors.

tau is tied to the distributed matrix V.

work

(local).

Workspace array of size k*(k -1)/2.

Output Parameters

v

t

(local)

Array of size nb_v * nb_v if storev = 'C', and mb_v * mb_v otherwise. It contains the k-by-k triangular factor of the block reflector associated with v. If direct = 'F', t is upper triangular;

if direct = 'B', t is lower triangular.

Application Notes

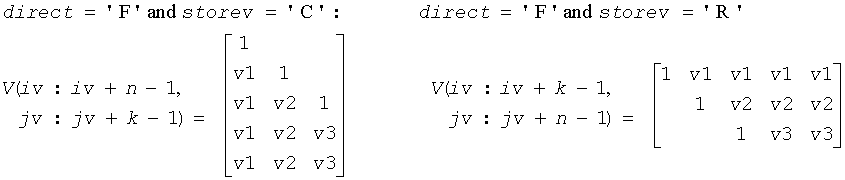
The shape of the matrix V and the storage of the vectors that define the H(i) is best illustrated by the following example with n = 5 and k = 3. The elements equal to 1 are not stored; the corresponding array elements are modified but restored on exit. The rest of the array is not used.

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

p?larft

See Also