?ggsvd

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-A30A127E-BD10-41C4-AAF7-BD045BE627B1

View Details

?ggsvd

Computes the generalized singular value decomposition of a pair of general rectangular matrices (deprecated).

Syntax

lapack_int LAPACKE_sggsvd( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int n, lapack_int p, lapack_int* k, lapack_int* l, float* a, lapack_int lda, float* b, lapack_int ldb, float* alpha, float* beta, float* u, lapack_int ldu, float* v, lapack_int ldv, float* q, lapack_int ldq, lapack_int* iwork );

lapack_int LAPACKE_dggsvd( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int n, lapack_int p, lapack_int* k, lapack_int* l, double* a, lapack_int lda, double* b, lapack_int ldb, double* alpha, double* beta, double* u, lapack_int ldu, double* v, lapack_int ldv, double* q, lapack_int ldq, lapack_int* iwork );

lapack_int LAPACKE_cggsvd( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int n, lapack_int p, lapack_int* k, lapack_int* l, lapack_complex_float* a, lapack_int lda, lapack_complex_float* b, lapack_int ldb, float* alpha, float* beta, lapack_complex_float* u, lapack_int ldu, lapack_complex_float* v, lapack_int ldv, lapack_complex_float* q, lapack_int ldq, lapack_int* iwork );

lapack_int LAPACKE_zggsvd( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int n, lapack_int p, lapack_int* k, lapack_int* l, lapack_complex_double* a, lapack_int lda, lapack_complex_double* b, lapack_int ldb, double* alpha, double* beta, lapack_complex_double* u, lapack_int ldu, lapack_complex_double* v, lapack_int ldv, lapack_complex_double* q, lapack_int ldq, lapack_int* iwork );

Include Files

mkl.h

Description

This routine is deprecated; use ggsvd3.

The routine computes the generalized singular value decomposition (GSVD) of an m-by-n real/complex matrix A and p-by-n real/complex matrix B:

U'*A*Q = D₁*(0 R), V'*B*Q = D₂*(0 R),

where U, V and Q are orthogonal/unitary matrices and U', V' mean transpose/conjugate transpose of U and V respectively.

Let k+l = the effective numerical rank of the matrix (A', B')', then R is a (k+l)-by-(k+l) nonsingular upper triangular matrix, D₁ and D₂ are m-by-(k+l) and p-by-(k+l) "diagonal" matrices and of the following structures, respectively:

If m-k-l≥0,

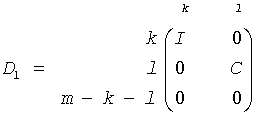
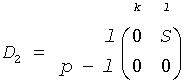
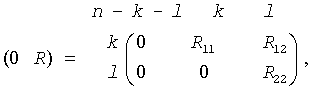
where

C = diag(alpha[k],..., alpha[k + l - 1])

S = diag(beta[k],...,beta[k + l - 1])

C² + S² = I

Nonzero element r_{i j} (1 ≤i≤j≤k + l) of R is stored in a[(i - 1) + (n - k - l + j - 1)*lda] for column major layout and in a[(i - 1)*lda + (n - k - l + j - 1)] for row major layout.

If m-k-l < 0,

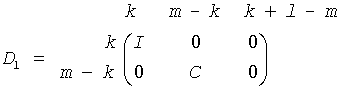
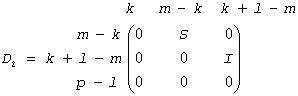
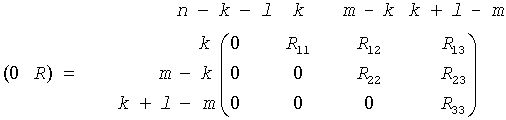
where

C = diag(alpha[k],..., alpha(m)),

S = diag(beta[k],...,beta[m - 1]),

C₂ + S₂ = I

On exit, the location of nonzero element r_{i j} (1 ≤i≤j≤k + l) of R depends on the value of i. For i≤m this element is stored in a[(i - 1) + (n - k - l + j - 1)*lda] for column major layout and in a[(i - 1)*lda + (n - k - l + j - 1)] for row major layout. For m < i≤k + l it is stored in b[(i - k - 1) + (n - k - l + j - 1)*ldb] for column major layout and in b[(i - k - 1)*ldb + (n - k - l + j - 1)] for row major layout.

The routine computes C, S, R, and optionally the orthogonal/unitary transformation matrices U, V and Q.

In particular, if B is an n-by-n nonsingular matrix, then the GSVD of A and B implicitly gives the SVD of A*B^-1:

A*B^-1 = U*(D₁*D₂^-1)*V'.

If (A', B')' has orthonormal columns, then the GSVD of A and B is also equal to the CS decomposition of A and B. Furthermore, the GSVD can be used to derive the solution of the eigenvalue problem:

A'**A*x = λ*B'*B*x.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

jobu

Must be 'U' or 'N'.

If jobu = 'U', orthogonal/unitary matrix U is computed.

If jobu = 'N', U is not computed.

jobv

Must be 'V' or 'N'.

If jobv = 'V', orthogonal/unitary matrix V is computed.

If jobv = 'N', V is not computed.

jobq

Must be 'Q' or 'N'.

If jobq = 'Q', orthogonal/unitary matrix Q is computed.

If jobq = 'N', Q is not computed.

m

The number of rows of the matrix A (m≥ 0).

n

The number of columns of the matrices A and B (n≥ 0).

p

The number of rows of the matrix B (p≥ 0).

a, b

Arrays:

a(size at least max(1, lda*n) for column major layout and max(1, lda*m) for row major layout) contains the m-by-n matrix A.

b(size at least max(1, ldb*n) for column major layout and max(1, ldb*p) for row major layout) contains the p-by-n matrix B.

lda

The leading dimension of a; at least max(1, m)for column major layout and max(1, n) for row major layout.

ldb

The leading dimension of b; at least max(1, p)for column major layout and max(1, n) for row major layout.

ldu

The leading dimension of the array u .

ldu≥ max(1, m) if jobu = 'U'; ldu≥ 1 otherwise.

ldv

The leading dimension of the array v .

ldv≥ max(1, p) if jobv = 'V'; ldv≥ 1 otherwise.

ldq

The leading dimension of the array q .

ldq≥ max(1, n) if jobq = 'Q'; ldq≥ 1 otherwise.

Output Parameters

k, l

On exit, k and l specify the dimension of the subblocks. The sum k+l is equal to the effective numerical rank of (A', B')'.

a

On exit, a contains the triangular matrix R or part of R.

b

On exit, b contains part of the triangular matrix R if m-k-l < 0.

alpha, beta

Arrays, size at least max(1, n) each.

Contain the generalized singular value pairs of A and B:

alpha(1:k) = 1,

beta(1:k) = 0,

and if m-k-l≥ 0,

alpha(k+1:k+l) = C,

beta(k+1:k+l) = S,

or if m-k-l < 0,

alpha(k+1:m)= C, alpha(m+1:k+l)=0

beta(k+1:m) = S, beta(m+1:k+l) = 1

and

alpha(k+l+1:n) = 0

beta(k+l+1:n) = 0.

u, v, q

Arrays:

u, size at least max(1, ldu*m).

If jobu = 'U', u contains the m-by-m orthogonal/unitary matrix U.

If jobu = 'N', u is not referenced.

v, size at least max(1, ldv*p).

If jobv = 'V', v contains the p-by-p orthogonal/unitary matrix V.

If jobv = 'N', v is not referenced.

q, size at least max(1, ldq*n).

If jobq = 'Q', q contains the n-by-n orthogonal/unitary matrix Q.

If jobq = 'N', q is not referenced.

iwork

On exit, iwork stores the sorting information.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = 1, the Jacobi-type procedure failed to converge. For further details, see subroutine tgsja.

Parent topic: Singular Value Decomposition: LAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?ggsvd