?hesvxx

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-45E49BC1-2339-4C96-979E-4D0333C49C6F

View Details

?hesvxx

Uses extra precise iterative refinement to compute the solution to the system of linear equations with a Hermitian indefinite coefficient matrix A applying the diagonal pivoting factorization.

Syntax

lapack_int LAPACKE_chesvxx( int matrix_layout, char fact, char uplo, lapack_int n, lapack_int nrhs, lapack_complex_float* a, lapack_int lda, lapack_complex_float* af, lapack_int ldaf, lapack_int* ipiv, char* equed, float* s, lapack_complex_float* b, lapack_int ldb, lapack_complex_float* x, lapack_int ldx, float* rcond, float* rpvgrw, float* berr, lapack_int n_err_bnds, float* err_bnds_norm, float* err_bnds_comp, lapack_int nparams, const float* params );

lapack_int LAPACKE_zhesvxx( int matrix_layout, char fact, char uplo, lapack_int n, lapack_int nrhs, lapack_complex_double* a, lapack_int lda, lapack_complex_double* af, lapack_int ldaf, lapack_int* ipiv, char* equed, double* s, lapack_complex_double* b, lapack_int ldb, lapack_complex_double* x, lapack_int ldx, double* rcond, double* rpvgrw, double* berr, lapack_int n_err_bnds, double* err_bnds_norm, double* err_bnds_comp, lapack_int nparams, const double* params );

Include Files

mkl.h

Description

The routine uses the diagonal pivoting factorization to compute the solution to a complex/double complex system of linear equations A*X = B, where A is an n-by-n Hermitian matrix, the columns of matrix B are individual right-hand sides, and the columns of X are the corresponding solutions.

Both normwise and maximum componentwise error bounds are also provided on request. The routine returns a solution with a small guaranteed error (O(eps), where eps is the working machine precision) unless the matrix is very ill-conditioned, in which case a warning is returned. Relevant condition numbers are also calculated and returned.

The routine accepts user-provided factorizations and equilibration factors; see definitions of the fact and equed options. Solving with refinement and using a factorization from a previous call of the routine also produces a solution with O(eps) errors or warnings but that may not be true for general user-provided factorizations and equilibration factors if they differ from what the routine would itself produce.

The routine ?hesvxx performs the following steps:

If fact = 'E', scaling factors are computed to equilibrate the system:

diag(s)*A*diag(s) *inv(diag(s))*X = diag(s)*B

Whether or not the system will be equilibrated depends on the scaling of the matrix A, but if equilibration is used, A is overwritten by diag(s)*A*diag(s) and B by diag(s)*B.
If fact = 'N' or 'E', the LU decomposition is used to factor the matrix A (after equilibration if fact = 'E') as

A = U*D*U^T, if uplo = 'U',

or A = L*D*L^T, if uplo = 'L',

where U or L is a product of permutation and unit upper (lower) triangular matrices, and D is a symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks.
If some D(i,i)=0, so that D is exactly singular, the routine returns with info = i. Otherwise, the factored form of A is used to estimate the condition number of the matrix A (see the rcond parameter). If the reciprocal of the condition number is less than machine precision, the routine still goes on to solve for X and compute error bounds.
The system of equations is solved for X using the factored form of A.
By default, unless params[0] is set to zero, the routine applies iterative refinement to get a small error and error bounds. Refinement calculates the residual to at least twice the working precision.
If equilibration was used, the matrix X is premultiplied by diag(r) so that it solves the original system before equilibration.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

fact

Must be 'F', 'N', or 'E'.

Specifies whether or not the factored form of the matrix A is supplied on entry, and if not, whether the matrix A should be equilibrated before it is factored.

If fact = 'F', on entry, af and ipiv contain the factored form of A. If equed is not 'N', the matrix A has been equilibrated with scaling factors given by s. Parameters a, af, and ipiv are not modified.

If fact = 'N', the matrix A will be copied to af and factored.

If fact = 'E', the matrix A will be equilibrated, if necessary, copied to af and factored.

uplo

Must be 'U' or 'L'.

Indicates whether the upper or lower triangular part of A is stored:

If uplo = 'U', the upper triangle of A is stored.

If uplo = 'L', the lower triangle of A is stored.

The number of linear equations; the order of the matrix A; n≥ 0.

nrhs

The number of right-hand sides; the number of columns of the matrices B and X; nrhs≥ 0.

a, af, b

Arrays: a(size max(lda*n)), af(size max(ldaf*n)), b, (size max(ldb*nrhs) for column major layout and max(ldb*n) for row major layout),.

The array a contains the Hermitian matrix A as specified by uplo. If uplo = 'U', the leading n-by-n upper triangular part of a contains the upper triangular part of the matrix A and the strictly lower triangular part of a is not referenced. If uplo = 'L', the leading n-by-n lower triangular part of a contains the lower triangular part of the matrix A and the strictly upper triangular part of a is not referenced.

The array af is an input argument if fact = 'F'. It contains the block diagonal matrix D and the multipliers used to obtain the factor U and L from the factorization A = U*D*U^T or A = L*D*L^T as computed by ?hetrf.

The array b contains the matrix B whose columns are the right-hand sides for the systems of equations.

lda

The leading dimension of the array a; lda≥ max(1,n).

ldaf

The leading dimension of the array af; ldaf≥ max(1,n).

ipiv

Array, size at least max(1, n). The array ipiv is an input argument if fact = 'F'. It contains details of the interchanges and the block structure of D as determined by ?sytrf.

If ipiv[k-1] > 0, rows and columns k and ipiv[k-1] were interchanged and D_k,k) is a 1-by-1 diagonal block.

If uplo = 'U' and ipiv[i] = ipiv[i - 1] = m < 0, D has a 2-by-2 diagonal block in rows and columns i and i + 1, and the i-th row and column of A were interchanged with the m-th row and column.

If uplo = 'L' and ipiv[i] = ipiv[i - 1] = m < 0, D has a 2-by-2 diagonal block in rows and columns i and i + 1, and the (i + 1)-st row and column of A were interchanged with the m-th row and column.

equed

Must be 'N' or 'Y'.

equed is an input argument if fact = 'F'. It specifies the form of equilibration that was done:

If equed = 'N', no equilibration was done (always true if fact = 'N').

if equed = 'Y', both row and column equilibration was done, that is, A has been replaced by diag(s)*A*diag(s).

Array, size (n). The array s contains the scale factors for A. If equed = 'Y', A is multiplied on the left and right by diag(s).

This array is an input argument if fact = 'F' only; otherwise it is an output argument.

If fact = 'F' and equed = 'Y', each element of s must be positive.

Each element of s should be a power of the radix to ensure a reliable solution and error estimates. Scaling by powers of the radix does not cause rounding errors unless the result underflows or overflows. Rounding errors during scaling lead to refining with a matrix that is not equivalent to the input matrix, producing error estimates that may not be reliable.

ldb

The leading dimension of the array b; ldb≥ max(1, n) for column major layout and ldb≥nrhs for row major layout.

ldx

The leading dimension of the output array x; ldx≥ max(1, n) for column major layout and ldx≥nrhs for row major layout.

n_err_bnds

Number of error bounds to return for each right hand side and each type (normwise or componentwise). See err_bnds_norm and err_bnds_comp descriptions in the Output Arguments section below.

nparams

Specifies the number of parameters set in params. If ≤ 0, the params array is never referenced and default values are used.

params

Array, size max(1,nparams). Specifies algorithm parameters. If an entry is less than 0.0, that entry is filled with the default value used for that parameter. Only positions up to nparams are accessed; defaults are used for higher-numbered parameters. If defaults are acceptable, you can pass nparams = 0, which prevents the source code from accessing the params argument.

params[0] : Whether to perform iterative refinement or not. Default: 1.0 (for single precision flavors), 1.0D+0 (for double precision flavors).

=0.0	No refinement is performed and no error bounds are computed.
=1.0	Use the extra-precise refinement algorithm.

(Other values are reserved for future use.)

params[1] : Maximum number of residual computations allowed for refinement.

Default	10
Aggressive	Set to 100 to permit convergence using approximate factorizations or factorizations other than LU. If the factorization uses a technique other than Gaussian elimination, the guarantees in err_bnds_norm and err_bnds_comp may no longer be trustworthy.

params[2] : Flag determining if the code will attempt to find a solution with a small componentwise relative error in the double-precision algorithm. Positive is true, 0.0 is false. Default: 1.0 (attempt componentwise convergence).

Output Parameters

x

Array, size max(1, ldx*nrhs) for column major layout and max(1, ldx*n) for row major layout.

If info = 0, the array x contains the solution n-by-nrhs matrix X to the original system of equations. Note that A and B are modified on exit if equed≠'N', and the solution to the equilibrated system is:

inv(diag(s))*X.

a

If fact = 'E' and equed = 'Y', overwritten by diag(s)*A*diag(s).

af

If fact = 'N', af is an output argument and on exit returns the block diagonal matrix D and the multipliers used to obtain the factor U or L from the factorization A = U*D*U^T or A = L*D*L^T.

b

If equed = 'N', B is not modified.

If equed = 'Y', B is overwritten by diag(s)*B.

s

This array is an output argument if fact≠'F'. Each element of this array is a power of the radix. See the description of s in Input Arguments section.

rcond

Reciprocal scaled condition number. An estimate of the reciprocal Skeel condition number of the matrix A after equilibration (if done). If rcond is less than the machine precision, in particular, if rcond = 0, the matrix is singular to working precision. Note that the error may still be small even if this number is very small and the matrix appears ill-conditioned.

rpvgrw

Contains the reciprocal pivot growth factor:

If this is much less than 1, the stability of the LU factorization of the (equlibrated) matrix A could be poor. This also means that the solution X, estimated condition numbers, and error bounds could be unreliable. If factorization fails with 0 < info≤n, this parameter contains the reciprocal pivot growth factor for the leading info columns of A.

berr

Array, size at least max(1, nrhs). Contains the component-wise relative backward error for each solution vector x_j, that is, the smallest relative change in any element of A or B that makes x_j an exact solution.

err_bnds_norm

Array of size nrhs*n_err_bnds. For each right-hand side, contains information about various error bounds and condition numbers corresponding to the normwise relative error, which is defined as follows:

Normwise relative error in the i-th solution vector

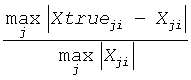
The array is indexed by the type of error information as described below. There are currently up to three pieces of information returned.

err=1

"Trust/don't trust" boolean. Trust the answer if the reciprocal condition number is less than the threshold sqrt(n)*slamch(ε) for chesvxx and sqrt(n)*dlamch(ε) for zhesvxx.

err=2

"Guaranteed" error bound. The estimated forward error, almost certainly within a factor of 10 of the true error so long as the next entry is greater than the threshold sqrt(n)*slamch(ε) for chesvxx and sqrt(n)*dlamch(ε) for zhesvxx. This error bound should only be trusted if the previous boolean is true.

err=3

Reciprocal condition number. Estimated normwise reciprocal condition number. Compared with the threshold sqrt(n)*slamch(ε) for chesvxx and sqrt(n)*dlamch(ε)for zhesvxx to determine if the error estimate is "guaranteed". These reciprocal condition numbers for some appropriately scaled matrix Z are:

Let z=s*a, where s scales each row by a power of the radix so all absolute row sums of z are approximately 1.

The information for right-hand side i, where 1 ≤i≤nrhs, and type of error err is stored in err_bnds_norm[(err-1)*nrhs + i - 1].

err_bnds_comp

Array of size nrhs*n_err_bnds. For each right-hand side, contains information about various error bounds and condition numbers corresponding to the componentwise relative error, which is defined as follows:

Componentwise relative error in the i-th solution vector:

The array is indexed by the type of error information as described below. There are currently up to three pieces of information returned for each right-hand side. If componentwise accuracy is not requested (params[2] = 0.0), then err_bnds_comp is not accessed.

err=1

"Trust/don't trust" boolean. Trust the answer if the reciprocal condition number is less than the threshold sqrt(n)*slamch(ε) for chesvxx and sqrt(n)*dlamch(ε) for zhesvxx.

err=2

"Guaranteed" error bpound. The estimated forward error, almost certainly within a factor of 10 of the true error so long as the next entry is greater than the threshold sqrt(n)*slamch(ε) for chesvxx and sqrt(n)*dlamch(ε) for zhesvxx. This error bound should only be trusted if the previous boolean is true.

err=3

Reciprocal condition number. Estimated componentwise reciprocal condition number. Compared with the threshold sqrt(n)*slamch(ε) for chesvxx and sqrt(n)*dlamch(ε) for zhesvxx to determine if the error estimate is "guaranteed". These reciprocal condition numbers for some appropriately scaled matrix Z are:

Let z=s*(a*diag(x)), where x is the solution for the current right-hand side and s scales each row of a*diag(x) by a power of the radix so all absolute row sums of z are approximately 1.

The information for right-hand side i, where 1 ≤i≤nrhs, and type of error err is stored in err_bnds_comp[(err-1)*nrhs + i - 1].

ipiv

If fact = 'N', ipiv is an output argument and on exit contains details of the interchanges and the block structure D, as determined by ssytrf for single precision flavors and dsytrf for double precision flavors.

equed

If fact≠'F', then equed is an output argument. It specifies the form of equilibration that was done (see the description of equed in Input Arguments section).

params

If an entry is less than 0.0, that entry is filled with the default value used for that parameter, otherwise the entry is not modified.

Return Values

This function returns a value info.

If info = 0, the execution is successful. The solution to every right-hand side is guaranteed.

If info = -i, the i-th parameter had an illegal value.

If 0 < info≤n: U_info,info is exactly zero. The factorization has been completed, but the factor U is exactly singular, so the solution and error bounds could not be computed; rcond = 0 is returned.

If info = n+j: The solution corresponding to the j-th right-hand side is not guaranteed. The solutions corresponding to other right-hand sides k with k > j may not be guaranteed as well, but only the first such right-hand side is reported. If a small componentwise error is not requested params[2] = 0.0, then the j-th right-hand side is the first with a normwise error bound that is not guaranteed (the smallest j such that for column major layout err_bnds_norm[j - 1] = 0.0 or err_bnds_comp[j - 1] = 0.0; or for row major layout err_bnds_norm[(j - 1)*n_err_bnds] = 0.0 or err_bnds_comp[(j - 1)*n_err_bnds] = 0.0). See the definition of err_bnds_norm and err_bnds_comp for err = 1. To get information about all of the right-hand sides, check err_bnds_norm or err_bnds_comp.

Parent topic: LAPACK Linear Equation Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?hesvxx

See Also