p?latrd

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-970AA850-96E7-47ED-9200-7A6EADAE1D0E

View Details

p?latrd

Reduces the first nb rows and columns of a symmetric/Hermitian matrix A to real tridiagonal form by an orthogonal/unitary similarity transformation.

Syntax

void pslatrd (char *uplo , MKL_INT *n , MKL_INT *nb , float *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , float *d , float *e , float *tau , float *w , MKL_INT *iw , MKL_INT *jw , MKL_INT *descw , float *work );

void pdlatrd (char *uplo , MKL_INT *n , MKL_INT *nb , double *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , double *d , double *e , double *tau , double *w , MKL_INT *iw , MKL_INT *jw , MKL_INT *descw , double *work );

void pclatrd (char *uplo , MKL_INT *n , MKL_INT *nb , MKL_Complex8 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , float *d , float *e , MKL_Complex8 *tau , MKL_Complex8 *w , MKL_INT *iw , MKL_INT *jw , MKL_INT *descw , MKL_Complex8 *work );

void pzlatrd (char *uplo , MKL_INT *n , MKL_INT *nb , MKL_Complex16 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , double *d , double *e , MKL_Complex16 *tau , MKL_Complex16 *w , MKL_INT *iw , MKL_INT *jw , MKL_INT *descw , MKL_Complex16 *work );

Include Files

mkl_scalapack.h

Description

The p?latrdfunction reduces nb rows and columns of a real symmetric or complex Hermitian matrix sub(A)= A(ia:ia+n-1, ja:ja+n-1) to symmetric/complex tridiagonal form by an orthogonal/unitary similarity transformation Q'*sub(A)*Q, and returns the matrices V and W, which are needed to apply the transformation to the unreduced part of sub(A).

If uplo = U, p?latrd reduces the last nb rows and columns of a matrix, of which the upper triangle is supplied;

if uplo = L, p?latrd reduces the first nb rows and columns of a matrix, of which the lower triangle is supplied.

This is an auxiliary function called by p?sytrd/p?hetrd.

Input Parameters

uplo

(global)

Specifies whether the upper or lower triangular part of the symmetric/Hermitian matrix sub(A) is stored:

= 'U': Upper triangular

= L: Lower triangular.

n

(global)

The number of rows and columns to be operated on, that is, the order of the distributed matrix sub(A). n ≥ 0.

nb

(global)

The number of rows and columns to be reduced.

a

Pointer into the local memory to an array of size lld_a * LOCc(ja+n-1).

On entry, this array contains the local pieces of the symmetric/Hermitian distributed matrix sub(A).

If uplo = U, the leading n-by-n upper triangular part of sub(A) contains the upper triangular part of the matrix, and its strictly lower triangular part is not referenced.

If uplo = L, the leading n-by-n lower triangular part of sub(A) contains the lower triangular part of the matrix, and its strictly upper triangular part is not referenced.

ia

(global)

The row index in the global matrix A indicating the first row of sub(A).

ja

(global)

The column index in the global matrix A indicating the first column of sub(A).

desca

(global and local) array of size dlen_. The array descriptor for the distributed matrix A.

iw

(global)

The row index in the global matrix W indicating the first row of sub(W).

jw

(global)

The column index in the global matrix W indicating the first column of sub(W).

descw

(global and local) array of size dlen_. The array descriptor for the distributed matrix W.

work

(local)

Workspace array of size nb_a.

Output Parameters

a

(local)

On exit, if uplo = 'U', the last nb columns have been reduced to tridiagonal form, with the diagonal elements overwriting the diagonal elements of sub(A); the elements above the diagonal with the array tau represent the orthogonal/unitary matrix Q as a product of elementary reflectors;

if uplo = 'L', the first nb columns have been reduced to tridiagonal form, with the diagonal elements overwriting the diagonal elements of sub(A); the elements below the diagonal with the array tau represent the orthogonal/unitary matrix Q as a product of elementary reflectors.

d

(local)

Array of size LOCc(ja+n-1).

The diagonal elements of the tridiagonal matrix T: d[i] = A(i+1,i+1), i = 0, 1, ..., LOCc(ja+n-1)-1. d is tied to the distributed matrix A.

e

(local)

Array of size LOCc(ja+n-1) if uplo = 'U', LOCc(ja+n-2) otherwise.

The off-diagonal elements of the tridiagonal matrix T:

e[i] = A(i + 1, i + 2) if uplo = 'U',

e[i] = A(i + 2, i + 1) if uplo = 'L',

i = 0, 1, ..., LOCc(ja+n-1)-1.

e is tied to the distributed matrix A.

tau

(local)

Array of size LOCc(ja+n-1). This array contains the scalar factors of the elementary reflectors. tau is tied to the distributed matrix A.

w

(local)

Pointer into the local memory to an array of size lld_w* nb_w. This array contains the local pieces of the n-by-nb_w matrix w required to update the unreduced part of sub(A).

Application Notes

If uplo = 'U', the matrix Q is represented as a product of elementary reflectors

Q = H(n)*H(n-1)*...*H(n-nb+1)

Each H(i) has the form

H(i) = I - tau*v*v' ,

where tau is a real/complex scalar, and v is a real/complex vector with v(i:n) = 0 and v(i-1) = 1; v(1:i-1) is stored on exit in A(ia:ia+i-1, ja+i), and tau in tau[ja+i-2].

If uplo = L, the matrix Q is represented as a product of elementary reflectors

Q = H(1)*H(2)*...*H(nb)

Each H(i) has the form

H(i) = I - tau*v*v' ,

where tau is a real/complex scalar, and v is a real/complex vector with v(1:i) = 0 and v(i+1) = 1; v(i+2: n) is stored on exit in A(ia+i+1: ia+n-1, ja+i-1), and tau in tau[ja+i-2].

The elements of the vectors v together form the n-by-nb matrix V which is needed, with W, to apply the transformation to the unreduced part of the matrix, using a symmetric/Hermitian rank-2k update of the form:

sub(A) := sub(A)-vw'-wv'.

The contents of a on exit are illustrated by the following examples with

n = 5 and nb = 2:

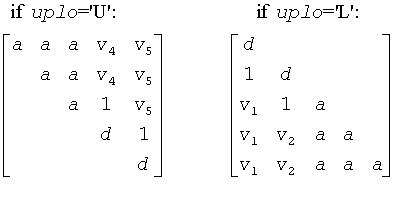
where d denotes a diagonal element of the reduced matrix, a denotes an element of the original matrix that is unchanged, and v_i denotes an element of the vector defining H(i).

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

p?latrd

See Also