p?tzrzf

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-0492967A-2902-4B0E-BF35-CE4BFF6BB410

View Details

p?tzrzf

Reduces the upper trapezoidal matrix A to upper triangular form.

Syntax

void pstzrzf (MKL_INT *m , MKL_INT *n , float *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , float *tau , float *work , MKL_INT *lwork , MKL_INT *info );

void pdtzrzf (MKL_INT *m , MKL_INT *n , double *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , double *tau , double *work , MKL_INT *lwork , MKL_INT *info );

void pctzrzf (MKL_INT *m , MKL_INT *n , MKL_Complex8 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , MKL_Complex8 *tau , MKL_Complex8 *work , MKL_INT *lwork , MKL_INT *info );

void pztzrzf (MKL_INT *m , MKL_INT *n , MKL_Complex16 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , MKL_Complex16 *tau , MKL_Complex16 *work , MKL_INT *lwork , MKL_INT *info );

Include Files

mkl_scalapack.h

Description

The p?tzrzffunction reduces the m-by-n (m ≤ n) real/complex upper trapezoidal matrix sub(A)= A(ia:ia+m-1, ja:ja+n-1) to upper triangular form by means of orthogonal/unitary transformations. The upper trapezoidal matrix A is factored as

A = (R 0)*Z,

where Z is an n-by-n orthogonal/unitary matrix and R is an m-by-m upper triangular matrix.

Input Parameters

m

(global) The number of rows in the matrix sub(A); (m≥0).

n

(global) The number of columns in the matrix sub(A) (n≥0).

a

(local)

Pointer into the local memory to an array of size lld_a*LOCc(ja+n-1). Contains the local pieces of the m-by-n distributed matrix sub (A) to be factored.

ia, ja

(global) The row and column indices in the global matrix A indicating the first row and the first column of the submatrix A, respectively.

desca

(global and local) array of size dlen_. The array descriptor for the distributed matrix A.

work

(local)

Workspace array of size of lwork.

lwork

(local or global) size of work, must be at least lwork≥mb_a*(mp0+nq0+mb_a), where

iroff = mod(ia-1, mb_a),

icoff = mod(ja-1, nb_a),

iarow = indxg2p(ia, mb_a, MYROW, rsrc_a, NPROW),

iacol = indxg2p(ja, nb_a, MYCOL, csrc_a, NPCOL),

mp0 = numroc (m+iroff, mb_a, MYROW, iarow, NPROW),

nq0 = numroc (n+icoff, nb_a, MYCOL, iacol, NPCOL)

NOTE:

mod(x,y) is the integer remainder of x/y.

indxg2p and numroc are ScaLAPACK tool functions; MYROW, MYCOL, NPROW and NPCOL can be determined by calling the function blacs_gridinfo.

If lwork = -1, then lwork is global input and a workspace query is assumed; the function only calculates the minimum and optimal size for all work arrays. Each of these values is returned in the first entry of the corresponding work array, and no error message is issued by pxerbla.

Output Parameters

a

On exit, the leading m-by-m upper triangular part of sub(A) contains the upper triangular matrix R, and elements m+1 to n of the first m rows of sub (A), with the array tau, represent the orthogonal/unitary matrix Z as a product of m elementary reflectors.

work[0]

On exit work[0] contains the minimum value of lwork required for optimum performance.

tau

(local)

Array of size LOCr(ia+m-1).

Contains the scalar factor of elementary reflectors. tau is tied to the distributed matrix A.

info

(global)

= 0: the execution is successful.

< 0:if the i-th argument is an array and the j-th entry, indexed j - 1, had an illegal value, then info = -(i*100+j); if the i-th argument is a scalar and had an illegal value, then info = -i.

Application Notes

The factorization is obtained by the Householder's method. The k-th transformation matrix, Z(k), which is or whose conjugate transpose is used to introduce zeros into the (m - k +1)-th row of sub(A), is given in the form

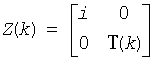
where

T(k) = i - tau*u(k)*u(k)',

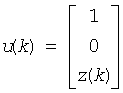
tau is a scalar and Z(k) is an (n - m) element vector. tau and Z(k) are chosen to annihilate the elements of the k-th row of sub(A). The scalar tau is returned in the k-th element of tau, indexed k-1, and the vector u(k) in the k-th row of sub(A), such that the elements of Z(k) are in a(k, m + 1),..., a(k, n). The elements of R are returned in the upper triangular part of sub(A). Z is given by

Z = Z(1) * Z(2) *... * Z(m).

Parent topic: Orthogonal Factorizations: ScaLAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

p?tzrzf

Syntax

Include Files

Description

Input Parameters

Output Parameters

Application Notes

See Also