Developer Reference for Intel® oneAPI Math Kernel Library for C
A newer version of this document is available. Customers should click here to go to the newest version.
?ggqrf
Computes the generalized QR factorization of two matrices.
Syntax
lapack_int LAPACKE_sggqrf (int matrix_layout, lapack_int n, lapack_int m, lapack_int p, float* a, lapack_int lda, float* taua, float* b, lapack_int ldb, float* taub);
lapack_int LAPACKE_dggqrf (int matrix_layout, lapack_int n, lapack_int m, lapack_int p, double* a, lapack_int lda, double* taua, double* b, lapack_int ldb, double* taub);
lapack_int LAPACKE_cggqrf (int matrix_layout, lapack_int n, lapack_int m, lapack_int p, lapack_complex_float* a, lapack_int lda, lapack_complex_float* taua, lapack_complex_float* b, lapack_int ldb, lapack_complex_float* taub);
lapack_int LAPACKE_zggqrf (int matrix_layout, lapack_int n, lapack_int m, lapack_int p, lapack_complex_double* a, lapack_int lda, lapack_complex_double* taua, lapack_complex_double* b, lapack_int ldb, lapack_complex_double* taub);
Include Files
- mkl.h
Description
The routine forms the generalized QR factorization of an n-by-m matrix A and an n-by-p matrix B as A = Q*R, B = Q*T*Z, where Q is an n-by-n orthogonal/unitary matrix, Z is a p-by-p orthogonal/unitary matrix, and R and T assume one of the forms:
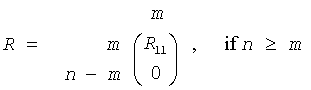
or
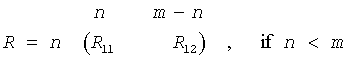
where R11 is upper triangular, and
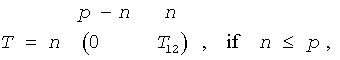
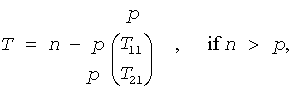
where T12 or T21 is a p-by-p upper triangular matrix.
In particular, if B is square and nonsingular, the GQR factorization of A and B implicitly gives the QR factorization of B-1A as:
B-1*A = ZT*(T-1*R) (for real flavors) or B-1*A = ZH*(T-1*R) (for complex flavors).
Input Parameters
- matrix_layout
-
Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).
- n
-
The number of rows of the matrices A and B (n≥ 0).
- m
-
The number of columns in A (m≥ 0).
- p
-
The number of columns in B (p≥ 0).
- a, b
-
Array a of size max(1, lda*m) for column major layout and max(1, lda*n) for row major layout contains the matrix A.
Array b of size max(1, ldb*p) for column major layout and max(1, ldb*n) for row major layout contains the matrix B.
- lda
-
The leading dimension of a; at least max(1, n) for column major layout and at least max(1, m) for row major layout.
- ldb
-
The leading dimension of b; at least max(1, n) for column major layout and at least max(1, p) for row major layout.
Output Parameters
- a, b
-
Overwritten by the factorization data as follows:
on exit, the elements on and above the diagonal of the array a contain the min(n,m)-by-m upper trapezoidal matrix R (R is upper triangular if n≥m);the elements below the diagonal, with the array taua, represent the orthogonal/unitary matrix Q as a product of min(n,m) elementary reflectors ;
if n≤p, the upper triangle of the subarray b(1:n, p-n+1:p ) contains the n-by-n upper triangular matrix T;
if n > p, the elements on and above the (n-p)th subdiagonal contain the n-by-p upper trapezoidal matrix T; the remaining elements, with the array taub, represent the orthogonal/unitary matrix Z as a product of elementary reflectors.
- taua, taub
-
Arrays, size at least max (1, min(n, m)) for taua and at least max (1, min(n, p)) for taub. The array taua contains the scalar factors of the elementary reflectors which represent the orthogonal/unitary matrix Q.
The array taub contains the scalar factors of the elementary reflectors which represent the orthogonal/unitary matrix Z.
Return Values
This function returns a value info.
If info=0, the execution is successful.
If info = -i, the i-th parameter had an illegal value.
Application Notes
The matrix Q is represented as a product of elementary reflectors
Q = H(1)H(2)...H(k), where k = min(n,m).
Each H(i) has the form
H(i) = I - τa*v*vT for real flavors, or
H(i) = I - τa*v*vH for complex flavors,
where τa is a real/complex scalar, and v is a real/complex vector with vj = 0 for 1 ≤j≤i - 1, vi = 1.
On exit, fori + 1 ≤j≤n, vj is stored in a[(j - 1) + (i - 1)*lda] for column major layout and in a[(j - 1)*lda + (i - 1)] for row major layout and τa is stored in taua[i - 1]
The matrix Z is represented as a product of elementary reflectors
Z = H(1)H(2)...H(k), where k = min(n,p).
Each H(i) has the form
H(i) = I - τb*v*vT for real flavors, or
H(i) = I - τb*v*vH for complex flavors,
where τb is a real/complex scalar, and v is a real/complex vector with vp - k + 1 = 1, vj = 0 for p - k + 1 ≤j≤p - 1, .
On exit, for 1 ≤j≤p - k + i - 1, vj is stored in b[(n - k + i - 1) + (j - 1)*ldb] for column major layout and in b[(n - k + i - 1)*ldb + (j - 1)] for row major layout and τb is stored in taub[i - 1].