?dbtrf

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-9FF79E0A-F1BC-4650-B5DA-B6D9DF7F7E8B

View Details

?dbtrf

Computes an LU factorization of a general band matrix with no pivoting (local blocked algorithm).

Syntax

void sdbtrf (MKL_INT *m , MKL_INT *n , MKL_INT *kl , MKL_INT *ku , float *ab , MKL_INT *ldab , MKL_INT *info );

void ddbtrf (MKL_INT *m , MKL_INT *n , MKL_INT *kl , MKL_INT *ku , double *ab , MKL_INT *ldab , MKL_INT *info );

void cdbtrf (MKL_INT *m , MKL_INT *n , MKL_INT *kl , MKL_INT *ku , MKL_Complex8 *ab , MKL_INT *ldab , MKL_INT *info );

void zdbtrf (MKL_INT *m , MKL_INT *n , MKL_INT *kl , MKL_INT *ku , MKL_Complex16 *ab , MKL_INT *ldab , MKL_INT *info );

Include Files

mkl_scalapack.h

Description

This function computes an LU factorization of a real m-by-n band matrix A without using partial pivoting or row interchanges.

This is the blocked version of the algorithm, calling BLAS Routines and Functions.

Input Parameters

m

The number of rows of the matrix A (m ≥ 0).

n

The number of columns in A(n ≥ 0).

kl

The number of sub-diagonals within the band of A(kl ≥ 0).

ku

The number of super-diagonals within the band of A(ku ≥ 0).

ab

Array of size ldab * n.

The matrix A in band storage, in rows kl+1 to 2kl+ku+1; rows 1 to kl need not be set. The j-th column of A is stored in the array ab as follows: ab[kl+ku+i-j+(j-1)*ldab] = A(i,j) for max(1,j-ku) ≤ i ≤ min(m,j+kl).

ldab

The leading dimension of the array ab.

(ldab ≥ 2kl + ku +1)

Output Parameters

ab

On exit, details of the factorization: U is stored as an upper triangular band matrix with kl+ku superdiagonals in rows 1 to kl+ku+1, and the multipliers used during the factorization are stored in rows kl+ku+2 to 2*kl+ku+1. See the Application Notes below for further details.

info

= 0: successful exit

< 0: if info = - i, the i-th argument had an illegal value,

> 0: if info = + i, the matrix element U(i,i) is 0. The factorization has been completed, but the factor U is exactly singular. Division by 0 will occur if you use the factor U for solving a system of linear equations.

Application Notes

The band storage scheme is illustrated by the following example, when m = n = 6, kl = 2, ku = 1:

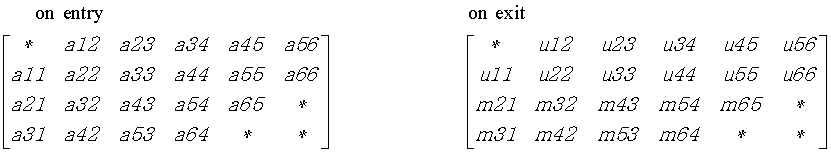
The function does not use array elements marked *.

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?dbtrf

Syntax

Include Files

Description

Input Parameters

Output Parameters

Application Notes

See Also