p?trcon

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-6AFDCD83-B8A1-4EB6-A502-8C8FA481BDEA

View Details

p?trcon

Estimates the reciprocal of the condition number of a triangular distributed matrix in either 1-norm or infinity-norm.

Syntax

void pstrcon (char *norm , char *uplo , char *diag , MKL_INT *n , float *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , float *rcond , float *work , MKL_INT *lwork , MKL_INT *iwork , MKL_INT *liwork , MKL_INT *info );

void pdtrcon (char *norm , char *uplo , char *diag , MKL_INT *n , double *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , double *rcond , double *work , MKL_INT *lwork , MKL_INT *iwork , MKL_INT *liwork , MKL_INT *info );

void pctrcon (char *norm , char *uplo , char *diag , MKL_INT *n , MKL_Complex8 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , float *rcond , MKL_Complex8 *work , MKL_INT *lwork , float *rwork , MKL_INT *lrwork , MKL_INT *info );

void pztrcon (char *norm , char *uplo , char *diag , MKL_INT *n , MKL_Complex16 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , double *rcond , MKL_Complex16 *work , MKL_INT *lwork , double *rwork , MKL_INT *lrwork , MKL_INT *info );

Include Files

mkl_scalapack.h

Description

The p?trconfunction estimates the reciprocal of the condition number of a triangular distributed matrix sub(A) = A(ia:ia+n-1, ja:ja+n-1), in either the 1-norm or the infinity-norm.

The norm of sub(A) is computed and an estimate is obtained for ||(sub(A))^-1||, then the reciprocal of the condition number is computed as

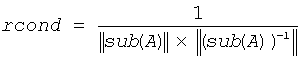
Input Parameters

norm

(global) Must be '1' or 'O' or 'I'.

Specifies whether the 1-norm condition number or the infinity-norm condition number is required.

If norm = '1' or 'O', then the 1-norm is used;

If norm = 'I', then the infinity-norm is used.

uplo

(global) Must be 'U' or 'L'.

If uplo = 'U', sub(A) is upper triangular. If uplo = 'L', sub(A) is lower triangular.

diag

(global) Must be 'N' or 'U'.

If diag = 'N', sub(A) is non-unit triangular. If diag = 'U', sub(A) is unit triangular.

n

(global) The order of the distributed matrix sub(A), (n≥0).

a

(local)

Pointer into the local memory to an array of size lld_a*LOCc(ja+n-1).

The array a contains the local pieces of the triangular distributed matrix sub(A).

If uplo = 'U', the leading n-by-n upper triangular part of this distributed matrix contains the upper triangular matrix, and its strictly lower triangular part is not referenced.

If uplo = 'L', the leading n-by-n lower triangular part of this distributed matrix contains the lower triangular matrix, and its strictly upper triangular part is not referenced.

If diag = 'U', the diagonal elements of sub(A) are also not referenced and are assumed to be 1.

ia, ja

(global) The row and column indices in the global matrix A indicating the first row and the first column of the matrix sub(A), respectively.

desca

(global and local) array of size dlen_. The array descriptor for the distributed matrix A.

work

(local)

The array work of size lwork is a workspace array.

lwork

(local or global) The size of the array work.

For real flavors:

lwork must be at least

lwork≥ 2*LOCr(n+mod(ia-1,mb_a))+LOCc(n+mod(ja-1,nb_a))+max(2, max(nb_a*max(1,iceil(NPROW-1, NPCOL)),

LOCc(n+mod(ja-1,nb_a))+nb_a*max(1,iceil(NPCOL-1, NPROW)))).

For complex flavors:

lwork must be at least

lwork≥ 2*LOCr(n+mod(ia-1,mb_a))+max(2, max(nb_a*iceil(NPROW-1, NPCOL),

LOCc(n+mod(ja-1,nb_a))+nb_a*iceil(NPCOL-1, NPROW))).

NOTE:

iceil(x,y) is the ceiling of x/y, and mod(x,y) is the integer remainder of x/y.

iwork

(local) Workspace array of size liwork. Used in real flavors only.

liwork

(local or global) The size of the array iwork; used in real flavors only. Must be at least

liwork≥LOCr(n+mod(ia-1,mb_a)).

rwork

(local)

Workspace array of size lrwork. Used in complex flavors only.

lrwork

(local or global) The size of the array rwork; used in complex flavors only. Must be at least

lrwork≥LOCc(n+mod(ja-1,nb_a)).

Output Parameters

rcond

(global)

The reciprocal of the condition number of the distributed matrix sub(A).

work[0]

On exit, work[0] contains the minimum value of lwork required for optimum performance.

iwork[0]

On exit, iwork[0] contains the minimum value of liwork required for optimum performance (for real flavors).

rwork[0]

On exit, rwork[0] contains the minimum value of lrwork required for optimum performance (for complex flavors).

info

(global) If info=0, the execution is successful.

info < 0:

If the i-th argument is an array and the j-th entry, indexed j - 1, had an illegal value, then info = -(i*100+j); if the i-th argument is a scalar and had an illegal value, then info = -i.

Parent topic: Estimating the Condition Number: ScaLAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

p?trcon

Syntax

Include Files

Description

Input Parameters

Output Parameters

See Also