?gebrd

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 6/24/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-03C78F41-D16C-4BFE-B087-BE4F5A6A0B9B

View Details

?gebrd

Reduces a general matrix to bidiagonal form.

Syntax

lapack_int LAPACKE_sgebrd( int matrix_layout, lapack_int m, lapack_int n, float* a, lapack_int lda, float* d, float* e, float* tauq, float* taup );

lapack_int LAPACKE_dgebrd( int matrix_layout, lapack_int m, lapack_int n, double* a, lapack_int lda, double* d, double* e, double* tauq, double* taup );

lapack_int LAPACKE_cgebrd( int matrix_layout, lapack_int m, lapack_int n, lapack_complex_float* a, lapack_int lda, float* d, float* e, lapack_complex_float* tauq, lapack_complex_float* taup );

lapack_int LAPACKE_zgebrd( int matrix_layout, lapack_int m, lapack_int n, lapack_complex_double* a, lapack_int lda, double* d, double* e, lapack_complex_double* tauq, lapack_complex_double* taup );

Include Files

mkl.h

Description

The routine reduces a general m-by-n matrix A to a bidiagonal matrix B by an orthogonal (unitary) transformation.

If m≥n, the reduction is given by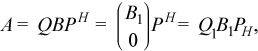

where B₁ is an n-by-n upper diagonal matrix, Q and P are orthogonal or, for a complex A, unitary matrices; Q₁ consists of the first n columns of Q.

If m < n, the reduction is given by

A = Q*B*P^H = Q*(B₁0)*P^H = Q₁*B₁*P₁^H,

where B₁ is an m-by-m lower diagonal matrix, Q and P are orthogonal or, for a complex A, unitary matrices; P₁ consists of the first m columns of P.

The routine does not form the matrices Q and P explicitly, but represents them as products of elementary reflectors. Routines are provided to work with the matrices Q and P in this representation:

If the matrix A is real,

to compute Q and P explicitly, call orgbr.
to multiply a general matrix by Q or P, call ormbr.

If the matrix A is complex,

to compute Q and P explicitly, call ungbr.
to multiply a general matrix by Q or P, call unmbr.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

m

The number of rows in the matrix A (m≥ 0).

n

The number of columns in A (n≥ 0).

a

Arrays:

a(size max(1, lda*n) for column major layout and max(1, lda*m) for row major layout) contains the matrix A.

lda

The leading dimension of a; at least max(1, m) for column major layout and at least max(1, n) for row major layout.

Output Parameters

a

If m≥n, the diagonal and first super-diagonal of a are overwritten by the upper bidiagonal matrix B. The elements below the diagonal, with the array tauq, represent the orthogonal matrix Q as a product of elementary reflectors, and the elements above the first superdiagonal, with the array taup, represent the orthogonal matrix P as a product of elementary reflectors.

If m < n, the diagonal and first sub-diagonal of a are overwritten by the lower bidiagonal matrix B. The elements below the first subdiagonal, with the array tauq, represent the orthogonal matrix Q as a product of elementary reflectors, and the elements above the diagonal, with the array taup, represent the orthogonal matrix P as a product of elementary reflectors.

d

Array, size at least max(1, min(m, n)).

Contains the diagonal elements of B.

e

Array, size at least max(1, min(m, n) - 1). Contains the off-diagonal elements of B.

tauq, taup

Arrays, size at least max (1, min(m, n)). The scalar factors of the elementary reflectors which represent the orthogonal or unitary matrices P and Q.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Application Notes

The computed matrices Q, B, and P satisfy QBP^H = A + E, where ||E||₂ = c(n)ε ||A||₂, c(n) is a modestly increasing function of n, and ε is the machine precision.

The approximate number of floating-point operations for real flavors is

(4/3)*n²*(3*m - n) for m≥n,

(4/3)*m²*(3*n - m) for m < n.

The number of operations for complex flavors is four times greater.

If n is much less than m, it can be more efficient to first form the QR factorization of A by calling geqrf and then reduce the factor R to bidiagonal form. This requires approximately 2*n²*(m + n) floating-point operations.

If m is much less than n, it can be more efficient to first form the LQ factorization of A by calling gelqf and then reduce the factor L to bidiagonal form. This requires approximately 2*m²*(m + n) floating-point operations.

Parent topic: Singular Value Decomposition: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?gebrd

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes