Visible to Intel only — GUID: GUID-CFE50177-6A1A-474D-8640-446F69CC03AD
Visible to Intel only — GUID: GUID-CFE50177-6A1A-474D-8640-446F69CC03AD
Limited-Memory Broyden-Fletcher-Goldfarb-Shanno Algorithm
The limited-memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) algorithm [Byrd2015] follows the algorithmic framework of an iterative solver with the algorithm-specific transformation T and set of intrinsic parameters  defined for the memory parameter m, frequency of curvature estimates calculation L, and step-length sequence
defined for the memory parameter m, frequency of curvature estimates calculation L, and step-length sequence  , algorithm-specific vector U and power d of Lebesgue space defined as follows:
, algorithm-specific vector U and power d of Lebesgue space defined as follows:
Transformation


where H is an approximation of the inverse Hessian matrix computed from m correction pairs by the Hessian Update Algorithm.
Convergence check: 
Intrinsic Parameters
For the LBFGS algorithm, the set of intrinsic parameters  includes the following:
includes the following:
Correction pairs

Correction index k in the buffer that stores correction pairs
Index of last iteration t of the main loop from the previous run
Average value of arguments for the previous L iterations

Average value of arguments for the last L iterations

Below is the definition and update flow of the intrinsic parameters  . The index is set and remains zero for the first
. The index is set and remains zero for the first  iterations of the main loop. Starting with iteration
iterations of the main loop. Starting with iteration  , the algorithm executes the following steps for each of L` iterations of the main loop:
, the algorithm executes the following steps for each of L` iterations of the main loop:

Choose a set of indices without replacement:
 ,
,  ,
,  ,
,  .
.Compute the sub-sampled Hessian

at the point
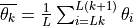 for the objective function using Hessians of its terms
for the objective function using Hessians of its terms

Compute the correction pairs
 :
:

- The set
 of intrinsic parameters is updated once per L iterations of the major loop and remains unchanged between iterations with the numbers that are multiples of L
of intrinsic parameters is updated once per L iterations of the major loop and remains unchanged between iterations with the numbers that are multiples of L A cyclic buffer stores correction pairs. The algorithm fills the buffer with pairs one-by-one. Once the buffer is full, it returns to the beginning and overwrites the previous correction pairs.
Hessian Update Algorithm
This algorithm computes the approximation of the inverse Hessian matrix from the set of correction pairs [Byrd2015].
For a given set of correction pairs  ,
,  :
:
Set

Iterate j from
 until k:
until k:Return H
Computation
The limited-memory BFGS algorithm is a special case of an iterative solver. For parameters, input, and output of iterative solvers, see Computation.
Algorithm Input
In addition to the input of the iterative solver, the limited-memory BFGS algorithm accepts the following optional input:
OptionalDataID |
Input |
|---|---|
correctionPairs |
A numeric table of size |
correctionIndices |
A numeric table of size |
averageArgumentLIterations |
A numeric table of size |
Algorithm Parameters
In addition to parameters of the iterative solver, the limited-memory BFGS algorithm has the following parameters:
Parameter |
Default Value |
Description |
|---|---|---|
algorithmFPType |
float |
The floating-point type that the algorithm uses for intermediate computations. Can be float or double. |
method |
defaultDense |
Performance-oriented computation method |
batchIndices |
NULL |
The numeric table of size
NOTE:
This parameter can be an object of any class derived from NumericTable, except for PackedTriangularMatrix, PackedSymmetricMatrix, and CSRNumericTable.
|
batchSize |
10 |
The number of observations to compute the stochastic gradient. The implementation of the algorithm ignores this parameter if the batchIndices numeric table is provided. If BatchSize equals the number of terms in the objective function, no random sampling is performed and all terms are used to calculate the gradient. |
correctionPairBatchSize |
100 |
The number of observations to compute the sub-sampled Hessian for correction pairs computation. The implementation of the algorithm ignores this parameter if the correctionPairIndices numeric table is provided. If correctionPairBatchSize equals the number of terms in the objective function, no random sampling is performed and all terms are used to calculate the Hessian matrix. |
correctionPairIndices |
NULL |
The numeric table of size
NOTE:
This parameter can be an object of any class derived from NumericTable, except for PackedTriangularMatrix, PackedSymmetricMatrix, and CSRNumericTable.
NOTE:
If the algorithm runs with no optional input data,
 rows of the table are used. Otherwise, it can use one more row, rows of the table are used. Otherwise, it can use one more row,
 in total. in total.
|
m |
10 |
The memory parameter. The maximum number of correction pairs that define the approximation of the Hessian matrix. |
L |
10 |
The number of iterations between calculations of the curvature estimates. |
stepLengthSequence |
A numeric table of size |
The numeric table of size
..note: The recommended data type for storing the step-length sequence is the floating-point type, either float or double, that the algorithm uses in intermediate computations. |
engine |
SharePtr< engines:: mt19937:: Batch>() |
Pointer to the random number generator engine that is used internally for random choosing terms from the objective function. |
Algorithm Output
In addition to the output of the iterative solver, the limited-memory BFGS algorithm calculates the following optional results:
OptionalDataID |
Output |
|---|---|
correctionPairs |
A numeric table of size |
correctionIndices |
A numeric table of size |
averageArgumentLIterations |
A numeric table of size |
Examples
C++ (CPU)
Batch Processing:
Python*
Batch Processing:


 where the rows represent correction pairs s and y. The row correctionPairs[j],
where the rows represent correction pairs s and y. The row correctionPairs[j],  , is a correction vector
, is a correction vector  , and the row correctionPairs[j],
, and the row correctionPairs[j],  , is a correction vector
, is a correction vector  .
. with 32-bit integer indexes. The first value is the index of correction pair t, the second value is the index of last iteration k from the previous run.
with 32-bit integer indexes. The first value is the index of correction pair t, the second value is the index of last iteration k from the previous run. , where row 0 represents average arguments for previous L iterations, and row 1 represents average arguments for last L iterations. These values are required to compute s correction vectors in the next step.
, where row 0 represents average arguments for previous L iterations, and row 1 represents average arguments for last L iterations. These values are required to compute s correction vectors in the next step. with 32-bit integer indices of terms in the objective function to be used in step 2 of the limited-memory BFGS algorithm. If no indices are provided, the implementation generates random indices.
with 32-bit integer indices of terms in the objective function to be used in step 2 of the limited-memory BFGS algorithm. If no indices are provided, the implementation generates random indices. with 32-bit integer indices to be used instead of random values. If no indices are provided, the implementation generates random indices.
with 32-bit integer indices to be used instead of random values. If no indices are provided, the implementation generates random indices. that contains the default step length equal to 1.
that contains the default step length equal to 1. or
or  : values of the step-length sequence
: values of the step-length sequence  for
for  .
. : the value of step length at each iteration
: the value of step length at each iteration 